Sécurisation des communications =============================== <br><br> *Ce document a été créé en collaboration avec l'IA Copilot intégrée au moteur de recherche Bing (elle-même reliée à ChatGPT), qui a été utilisée pour transposer le cours correspondant (accessible [ici](securisation-communications)) en un diaporama.* --- # Introduction ---- # Introduction - Les objets numériques sont souvent la cible d'**attaques**. - La **cybersécurité** développe des méthodes **pour éviter ou détecter** ces actes malveillants. - C'est **enjeu majeur du 21ème siècle** (scientifique et technologique, économique, politique, militaire, etc.) ---- # Introduction - Le chiffre de César est un exemple ancien de chiffrement par décalage. - La valeur de ce décalage est appelé la **clé de chiffrement** <img class="centre image-responsive image-encadree" src="data/cesar.svg" alt="Schéma du chiffrement symétrique" width="400"> <p><small>Crédit : <a href="https://commons.wikimedia.org/wiki/File:Caesar3.svg">Cepheus</a>, Domaine public, via Wikimedia Commons</small></p> ---- # Introduction - Méthodes de chiffrement actuelles : beaucoup plus sophistiquées mais toujours basées sur **une ou plusieurs clés de chiffrement**. - Chiffrement : utilisé quotidiennement dans de nombreuses applications : vous l'utilisez des dizaines de fois par jour (des idées ?) - Deux grandes catégories de chiffrement : - les **chiffrements symétriques** - les **chiffrements asymétriques**. --- # Chiffrement symétrique ---- # Chiffrement symétrique <img class="r-stretch centre image-responsive image-encadree" src="data/chiffrement_symetrique.png" alt="Schéma du chiffrement symétrique"> <p><small>Crédit : <a href="https://commons.wikimedia.org/wiki/File:Chiffrement_sym%C3%A9trique.png">MarcT0K (icônes par JGraph)</a>, <a href="https://creativecommons.org/licenses/by-sa/4.0">CC BY-SA 4.0</a>, via Wikimedia Commons</small></p> - Aussi appelé chiffrement **à clé secrète** - Chiffrement dit **symétrique** car c'est le **même clé** qui permet de **chiffrer *et*** de **déchiffrer** (ex: chiffre de César) ---- # Chiffrement symétrique - Forme de chiffrement la plus ancienne. - Clé de chiffrement : - doit **rester secrète** - être suffisamment **complexe** pour résister à une attaque par **force brute**. > Qu'est-ce qu'une attaque par *force brute* ? ---- ## Chiffrement XOR - Chiffrement XOR = algorithme de chiffrement symétrique plus évolué. - Basé sur l'opérateur logique XOR. | **$x$** | $y$ | $x \oplus y$ | |---------|-----|:-------------:| | **0** | 0 | 0 | | **0** | 1 | 1 | | **1** | 0 | 1 | | **1** | 1 | 0 | - Utilisation d'une clé secrète pour chiffrer et déchiffrer un message. Exemple : message = "MOUNIER" et clé = "INFO". ---- ## Chiffrement XOR - **Pour chiffrer** : opération XOR bit à bit entre le message et la clé. <div style="font-size:0.8em"> <table class="tg"> <tbody> <tr> <td style="width:100px">Message</td> <td>M</td> <td>O</td> <td>U</td> <td>N</td> <td>I</td> <td>E</td> <td>R</td> </tr> <tr> <td>Clé</td> <td>i</td> <td>n</td> <td>f</td> <td>o</td> <td>i</td> <td>n</td> <td>f</td> </tr> <tr> <td>Message</td> <td>01001101</td> <td>01001111</td> <td>01010101</td> <td>01001110</td> <td>01001001</td> <td>01000101</td> <td>01010010</td> </tr> <tr> <td>Clé</td> <td>01101001</td> <td>01101110</td> <td>01100110</td> <td>01101111</td> <td>01101001</td> <td>01101110</td> <td>01100110</td> </tr> <tr> <td>Message chiffré (XOR)</td> <td>00100100</td> <td>00100001</td> <td>00110011</td> <td>00100001</td> <td>00100000</td> <td>00101011</td> <td>00110100</td> </tr> <tr> <td>Message chiffré</td> <td>24</td> <td>21</td> <td>33</td> <td>21</td> <td>20</td> <td>2B</td> <td>34</td> </tr> <tr> <td>Message chiffré</td> <td>$</td> <td>!</td> <td>3</td> <td>!</td> <td>(espace)</td> <td>+</td> <td>4</td> </tr> </tbody> </table> </div> ---- ## Chiffrement XOR et amélioration - **Pour déchiffer** : à nouveau XOR bit à bit entre le message chiffré et la clé (car $(x \oplus y) \oplus y = x$) - Pas infaillible si on utilise toujours la même clé et qu'on l'étend pour atteindre la taille du message - Mais une amélioration, appelée **masque jetable** ou **chiffre de Vernam**, permet d'obtenir un chiffrement incassable : - clé : aussi longue que le message à chiffrer - caractères de la clé : choisis de façon totalement aléatoire - chaque clé utilisée qu'une seule fois. ---- ## Chiffrement XOR et amélioration - **Chiffre de Vernam** (masque jetable) : inutilisable en pratique car générer aléatoirement une *nouvelle* clé à chaque chiffrement n'est pas possible - Il existe des chiffrements incassables qui permettent de conserver la même clé pour toute une série d'échanges, exemple : chiffrement AES ---- ## Chiffrement AES - Chiffrement **AES** (*Advanced Encryption Standard*, soit « norme de chiffrement avancé ») = **chiffrement *symétrique* le plus utilisé**. - Très similaire au chiffrement XOR ou masque jetable : - clé aléatoire de taille 128, 192 ou 256 bits. - clé utilisée pour transformer le message à chiffrer mais avec davantage d'opérations qu'un simple XOR - clé utilisée pour déchiffrer - Aucune attaque connue efficace ---- ## Chiffrement AES - Seule possibilité : attaque par *force brute* mais ... - Avec une clé de 256 bits (pour le chiffrement AES-256) - $2^{256}$ clés possibles soit $\simeq 1.16\times 10^{77}$ clés à tester. - en supposant que l'on puisse tester 1 000 milliards de clés par seconde - il faudra plus d'un milliard de milliards de milliards de milliards de fois l'âge de l'univers pour tester toutes les clés possibles 🤯🤯🤯 - Utilisé : - par la NSA pour ses documents "secrets défense" - dans les gestionnaires de mots de passe - pour chiffrer des bases de données ---- ## Point faible des chiffrements symétriques - **L'échange de la clé !** - *Comment s'échanger la clé servant à chiffrer les communications lorsque le canal n'est pas encore sécurisé ?* - Ce problème est résolu par l'utilisation de chiffrements *asymétriques*. --- # Chiffrement asymétrique ---- # Chiffrement asymétrique - Aussi appelé chiffrement **à clé publique** - Cette clé publique est connue de tous - Associée à une **clé privée** qui n'est jamais partagée - Chiffrement utilisé dans des protocoles qui permettent de sécuriser des communications, par exemple : Diffie-Hellman, RSA ---- ## Échange de clés de Diffie-Hellmann - Protocole *asymétrique* présenté par Whitfield Diffie et Martin Hellmann en 1976. - Permet à deux personnes de s'échanger des secrets même en étant écoutés en permanence par un espion ! - Concrètement : - Permet de construire une clé secrète partagée - Pour la construire : les échanges ne sont pas chiffrés - Un troisième participant qui écoute tous les échanges ne peut pas déterminer la clé secrète. - Basé sur des concepts mathématiques (voir vidéo de David Louapre : https://youtu.be/1Yv8m398Fv0) ---- ## Échange de clés de Diffie-Hellmann - Analogie avec des pots de peintures pour comprendre le principe. <img class="r-stretch centre image-responsive image-encadree" src="data/diffie_hellmann.svg" alt="Illustration conceptuelle de l'échange de clef Diffie-Hellman"> <p><small>Crédit : <a href="https://commons.wikimedia.org/wiki/File:Diffie-Hellman_Key_Exchange_(fr).svg">Idée originale : A.J. Han VinckVersion vectorielle : FlugaalTraduction : Dereckson</a>, Domaine public, via Wikimedia Commons</small></p> ---- <img class="r-stretch centre image-responsive image-encadree" src="data/diffie_hellmann.svg" alt="Illustration conceptuelle de l'échange de clef Diffie-Hellman"> <ul class="r-stack"> <li class="fragment fade-in-then-out" data-fragment-index="0"><strong>Étape 1</strong> : Alice et Bob choisissent au préalable une peinture commune, ici le jaune. Cette couleur est connue de tous, y compris de l'intrus Ève.</li> <li class="fragment fade-in-then-out" data-fragment-index="1"><strong>Étape 2</strong> : Alice choisit une autre couleur secrète (ici du rouge). Elle mélange la peinture commune et sa couleur secrète et obtient de l'orange. Alice envoie la couleur orange à Bob. La couleur orange est connue d'Ève.</li> <li class="fragment fade-in-then-out" data-fragment-index="2"><strong>Étape 3</strong> : Bob fait de même : il choisit une couleur secrète (ici du cyan) qu'il mélange à la peinture commune et il obtient du bleu. Bob envoie sa couleur bleu à Alice. La couleur bleue est connue d'Ève.</li> <li class="fragment fade-in-then-out" data-fragment-index="3"><strong>Étape 4</strong> : Alice prend la couleur reçue (le bleu) qu'elle mélange avec sa couleur secrète rouge. Elle obtient une couleur brune.</li> <li class="fragment fade-in-then-out" data-fragment-index="4"><strong>Étape 5</strong> : Bob prend la couleur reçue (le orange) qu'il mélange avec sa couleur secrète cyan. Il obtient la même couleur brune.</li> <li class="fragment" data-fragment-index="5">À l'issue du protocole : Alice et Bob possèdent la même couleur brune qui représente la <strong>couleur secrète partagée</strong></li> </ul> ---- <img class="r-stretch centre image-responsive image-encadree" src="data/diffie_hellmann.svg" alt="Illustration conceptuelle de l'échange de clef Diffie-Hellman"> **Sur quoi repose la sécurité du protocole ?** - Si on connaît un mélange de deux couleurs et l'une des deux couleurs utilisées, il est difficile de retrouver l'autre - Ici : Ève connaît les couleurs publiques (orange et bleue) et la couleur commune de départ mais impossible de retrouver les couleurs secrètes (rouge et cyan) : elle ne peut donc pas trouver la couleur brune secrète. ---- <img class="r-stretch centre image-responsive image-encadree" src="data/diffie_hellmann.svg" alt="Illustration conceptuelle de l'échange de clef Diffie-Hellman"> **L'analogie fonctionne car :** - si on connait une couleur $x$ et la couleur du mélange $M(x,y)$ entre les couleurs $x$ et $y$, il est « difficile » de déterminer exactement la nuance de couleur $y$ - le mélange de trois couleurs donne la même couleur peut importe l'ordre dans lequel on fait le mélange : $M(M(x,y),z) = M(M(x,z),y)$. ---- ## Échange de clés de Diffie-Hellmann - Clé secrète partagée (couleur commune) : ensuite utilisée pour chiffrer et déchiffrer les communications de manière sûre. - Concrètement : - les couleurs sont remplacés par des entiers et un nombre premier, tous très grands - des calculs sur ces nombres permettent de faire les "mélanges" - à partir des nombres obtenus : très difficile de retrouver ceux de départ - voir vidéo de David Louapre (https://youtu.be/1Yv8m398Fv0) ---- ## Échange de clés de Diffie-Hellmann - **Point faible** : ne permet pas d'**authentifier** les participants. - Autrement dit : - Ève peut se faire passer pour Bob auprès d'Alice, et pour Alice auprès de Bob - C'est l'**attaque de l'homme au milieu**, ou **man in the middle**. - Autres chiffrements asymétriques, comme le chiffrement RSA, règlent ce problème d'authentification. ---- ## RSA : le *chiffrement* - **RSA** = système de chiffrement *asymétrique* implémenté en **1978** - Du nom de ses trois inventeurs : les cryptologues Ronald **Rivest**, Adi **Shamir** et Leonard **Adleman** - Repose sur l'utilisation d'un couple de clés : - une **clé publique** notée $C^{\text{pub}}$ - et une **clé privée** notée $C^{\text{priv}}$ - Une clé sert à chiffrer le message et l'autre à le déchiffrer. ---- ## RSA : le *chiffrement* - Les clés sont générées de manière complexe, basée sur des théorèmes d'arithmétique. - Elles sont liées de la façon suivante : $$C^{\text{pub}}(C^{\text{priv}}(m)) = C^{\text{priv}}(C^{\text{pub}}(m)) = m$$ - Connaissant l'une, il est impossible de déduire l'autre ou de déduire le message original (= on ne peut pas trouver $m$ en connaissant $C^{\text{pub}}(m)$ ou $C^{\text{priv}}(m)$) - En utilisant ces deux clés, Alice peut envoyer un message chiffré à Bob. ---- ## RSA : le *chiffrement*  **Étape 1** - Bob fabrique sa clé publique et sa clé privée. - Il envoie sa clé publique à Alice et garde sa clé privée secrète. ---- ## RSA : le *chiffrement*  **Étape 2** - Alice chiffre son message $m$ avec la clé publique de Bob. - Elle envoie le message chiffré $C^{\text{pub}}_\text{Bob}(m)$ à Bob. ---- ## RSA : le *chiffrement*  **Étape 3** - Bob utilise sa clé privée pour déchiffrer le message d'Alice - Bob peut lire le message original. ---- ## RSA : le *chiffrement*  - Si Ève intercepte le message chiffré (étape 2), elle ne peut rien en faire sans la clé privée de Bob - La communication est sécurisée ---- ## RSA : le *chiffrement* - En pratique, RSA est lourd en calculs pour chiffrer et déchiffrer des messages : cela ralentit les échanges - Donc RSA est difficilement utilisable en pratique pour échanger des données volumineuses - Mais il peut être **utilisé pour échanger une clé symétrique** en toute sécurité, et, une fois la clé échangée avec RSA, le reste des commnications se poursuit avec un chiffrement symétrique beaucoup plus efficace (ex : AES) ---- ## RSA : le *chiffrement* **Comment utiliser RSA pour s'échanger une clé symétrique ?** - Alice choisit comme message $m$ une clé symétrique (AES) - Elle chiffre cette clé symétrique avec la clé publique de Bob.  - Bob déchiffre la clé avec sa clé privée. - Ensuite, ils utilisent cette clé symétrique pour chiffrer leurs communications. ---- ## RSA : l'*authentification* - La partie *chiffrement* de RSA décrite à l'instant (tout comme Diffie-Hellman) ne garantit pas l'identité des participants. - Ils sont vulnérables à l'attaque **man in the middle**  - Ève peut se faire passer pour Bob auprès d'Alice et pour Alice auprès de Bob ---- ## RSA : l'*authentification* - L'**authentification** assure que chaque participant s'adresse à la bonne personne. - Le chiffrement RSA tel qu'on l'a vu est complété par un mécanisme permettant de gérer l'**authentification des participants**. ---- ## RSA : l'*authentification* - **Solution** : **certificats** et **autorités de certification** - Un certificat, délivré par une autorité de certification (AC), prouve l'identité d'un participant. - Le certificat est obtenu en chiffrant la clé publique d'un participant avec la clé privée de l'AC. ---- ## RSA : l'*authentification* **Étape 1 : Demande de certificat** - Bob demande un certificat à une autorité de certification (AC). - L'AC : - vérifie qu'il s'agit bien de Bob (on ne détaille pas) - chiffre la clé publique de Bob avec sa clé privée pour obtenir le **certificat** : $s = C^{\text{priv}}\_{\text{AC}}(C^{\text{pub}}_\text{Bob})$ - Bob peut communiquer le certificat (c'est un fichier) à ses interlocuteurs pour justifier qu'il s'agit bien de lui ---- ## RSA : l'*authentification* **Étape 2 : Communication** - Alice veut communiquer avec Bob, elle le contacte - Bob transmet : - sa clé publique $C^{\text{pub}}_\text{Bob}$ - **et son certificat $s$** ---- ## RSA : l'*authentification* **Étape 3 : Vérification du certificat** - Alice utilise la clé publique de l'AC (en qui elle a aussi confiance) pour vérifier le certificat : $$C^{\text{pub}}\_\text{AC}(s)=\underbrace{C^{\text{pub}}\_\text{AC}(C^{\text{priv}}\_\text{AC}}\_{\text{s'annulent}}(C^{\text{pub}}\_\text{Bob}))=C^{\text{pub}}\_\text{Bob}$$ - Si le résultat correspond à la clé publique de Bob, Alice peut être certaine de l'identité de Bob. ---- ## RSA : l'*authentification* **Étape 4 : Initialisation de la communication** - Alice peut commencer la communication en utilisant la clé publique de Bob ou en utilisant le protocole de Diffie-Hellmann pour établir une clé partagée. ---- ## RSA : l'*authentification* - Lorsque l'autorité de certification chiffre la clé publique de Bob avec sa clé privée ($s = C^{\text{priv}}\_{\text{AC}}(C^{\text{pub}}_\text{Bob})$), on dit qu'elle **signe** la clé publique de Bob, d'où le nom $s$. - Ce mécanisme est aussi utilisé pour les **signatures électroniques** --- # Le protocole HTTPS ---- ## Introduction - Le protocole **HTTP** présente des vulnérabilités en termes de sécurité : - la transmission en clair des informations - l'absence de mécanisme d'authentification (donc vulnérabilité à l'attaque de l'homme au milieu). - Protocole **HTTPS** (Hypertext Transfer Protocol **Secure**) : - chiffre tous les échanges sur le Web - combinaison d'un chiffrement **asymétrique** **et** d'un chiffrement **symétrique** ---- ## HTTPS - HTTPS = - protocole HTTP - **et** une couche de **cryptographie** grâce au **protocole TLS** (Transport Layer Security). - TLS permet d'*authentifier* le serveur et d'établir une *clé de chiffrement symétrique*, appelée **clé de session** pour sécuriser les échanges. - La suite des échanges se fait suivant le protocole HTTP en chiffrant les messages avec la clé de session. ---- ### Fonctionnement de HTTPS <img class="r-stretch" alt="Fonctionnement du protocole HTTPS" src="data/tls.svg"> <!--  --> <ul class="r-stack"> <li class="fragment fade-in-then-out" data-fragment-index="0"><strong>Étape 1</strong> : Le client envoie un message "Hello" au serveur pour demander une connexion sécurisée.</li> <li class="fragment fade-in-then-out" data-fragment-index="1"><strong>Étape 2</strong> : Le serveur répond avec sa clé publique et son certificat (qui est la signature de la clé publique par l'AC)</li> <li class="fragment fade-in-then-out" data-fragment-index="2"><strong>Étape 3</strong> : Le client valide le certificat en utilisant la clé publique de l'AC comme vu précédemment (en pratique les navigateurs disposent des clés publiques des AC)</li> <li class="fragment fade-in-then-out" data-fragment-index="3"><strong>Étape 4</strong> : Le client et le serveur utilisent un algo de chiffrement à clé publique (asymétrique) pour établir une <strong>clé de session</strong> partagée.</li> <li class="fragment" data-fragment-index="4"><strong>Étape 5</strong> : Pour la suite : client et serveur utilisent cette clé dans un chiffrement symétrique (AES) selon le protocole HTTP mais avec des requêtes et réponses chiffrées.</li> </ul> ---- ### Authentification dans le navigateur - 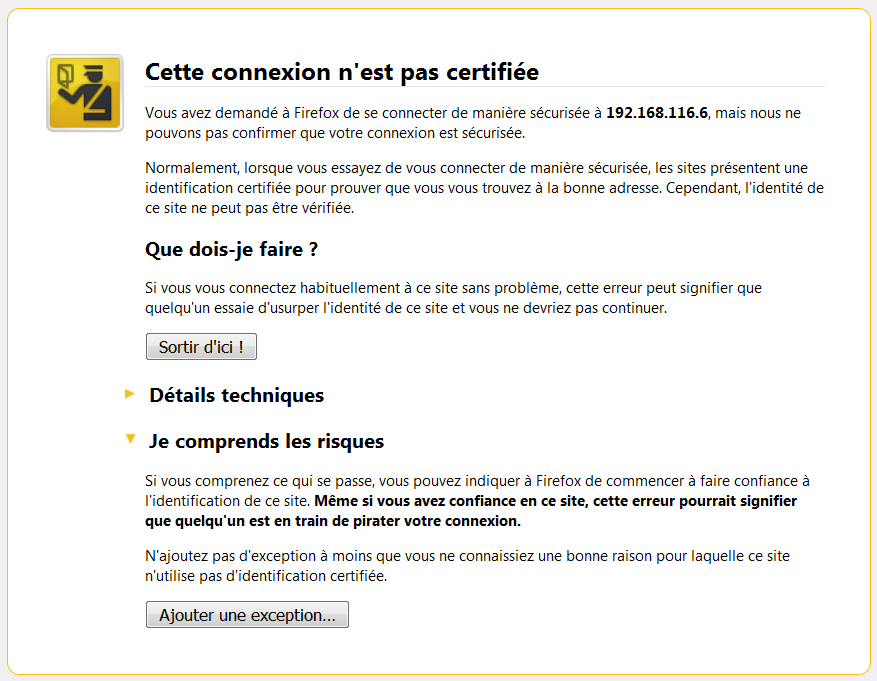En cas d'échec d'authentification (étape 3), le navigateur affiche un avertissement à l'utilisateur. <img class="r-stretch" alt="message d'alerte d'une connexion non certifiée" src="data/echec_authentification.png"> <!--  --> <p><small>Crédit : <a href="https://commons.wikimedia.org/wiki/File:Caesar3.svg">Cepheus</a>, Domaine public, via Wikimedia Commons</small></p> ---- ### Authentification dans le navigateur - Si le certificat est expiré, le navigateur alerte également l'utilisateur.  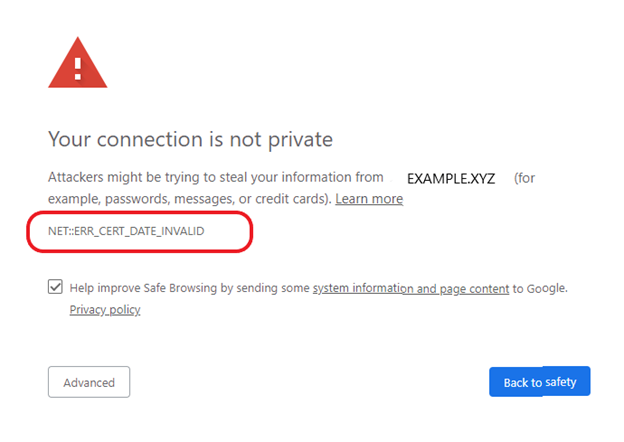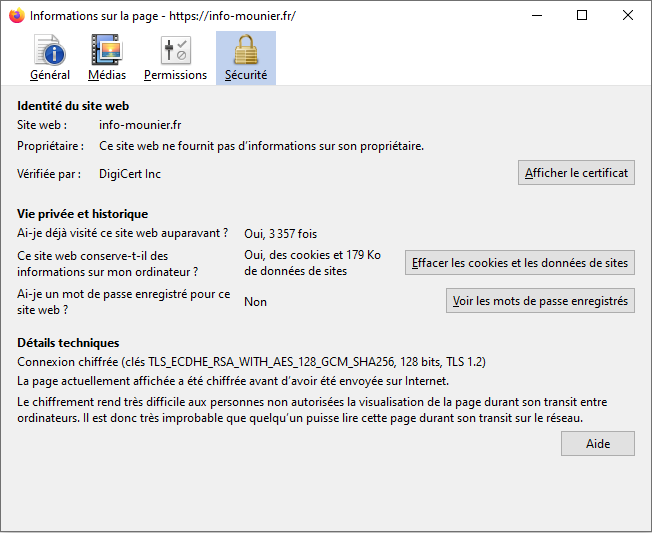---- ### Authentification dans le navigateur - Il est possible de consulter le certificat d'un site HTTPS dans le navigateur (ex : `info-mounier.fr`) <img class="r-stretch" alt="certificat du site info-mounier.fr" src="data/certificat_info-mounier.png"> <!--  --> ---- ### Authentification dans le navigateur - L'AC est DigiCert Inc - On voit comment est chiffrée la connexion dans les détails techniques : ```plaintext TLS_ECDHE_RSA_WITH_AES_128_GCM_SHA256, 128 bits, TLS 1.2 ``` - Donc : - Protocole TLS utilisé (version 1.2) - `ECDHE` (*Elliptic Curve Diffie-Hellmann Ephemeral*) : la clé de session a été échangée par le protocole de Diffie-Hellmann (dans une variante utilisant les *courbes elliptiques* comme problème mathématique sous-jacent). - Authentification : assurée par le protocole RSA. - Le chiffrement symétrique (grâce à la clé de session) : assuré par l'algorithme AES128 --- # Bilan - Il existe deux familles de chiffrement : **symétrique** et **asymétrique**. - Chiffrement **symétrique** : - dit chiffrement **à clé secrète** - cette clé, partagée par les deux participants, sert à chiffrer et déchiffrer - exemple : AES - point faible : l'échange de la clé - Chiffrement **asymétrique** : - dit chiffrement **à clé publique** - basé sur des paires de clés publiques et privées - exemples : Diffie-Helmman, RSA ---- # Bilan - Le protocole d'**échange de clés de Diffie-Hellman** permet à deux participants de s'échanger de manière sécurisée une clé partagée même si le canal de communication est écouté - Mais ce protocole ne permet pas l'**authentification** donc est vulnérable à l'**attaque de l'homme au milieu** - L'algorithme **RSA**, basé sur une paire (clé privé, clé publique), permet de chiffrer les échanges mais ajoute une couche d'authentification grâce à des **autorités de certification** qui produisent des **certificats** attestant de l'identité d'un participant. ---- # Bilan - Le protocole **HTTPS** ajoute une **couche de sécurité** au protocole HTTP grâce au **protocole TLS**. - TLS : - utilise RSA pour sécuriser le début de la communication et authentifier le serveur - implémente l'échange d'une **clé de session** via Diffie-Hellmann ou RSA. - HTTP : - Lorsque les deux participants disposent de cette clé, la suite des échanges (requêtes/réponses HTTP) se fait avec un chiffrement symétrique, beaucoup plus rapide, tel que **AES**. ---- # Bilan - Tous les algos de chiffrement sont basés sur des clés, qui s'allongent au fur et à mesure de l'augmentation des performances des ordinateurs (pour éviter des attaques par *force brute*). - L'arrivée d'un ordinateur quantique rendrait instantanément obsolètes tous les chiffrements actuels. --- **Références** : - Articles Wikipédia : [Cryptographie symétrique](https://fr.wikipedia.org/wiki/Cryptographie_sym%C3%A9trique), [Cryptographie asymétrique](https://fr.wikipedia.org/wiki/Cryptographie_asym%C3%A9trique), [Échange de clés de Diffie-Hellmann](https://fr.wikipedia.org/wiki/%C3%89change_de_cl%C3%A9s_Diffie-Hellman), [Chiffrement RSA](https://fr.wikipedia.org/wiki/Chiffrement_RSA), [Attaque de l'homme du milieu](https://fr.wikipedia.org/wiki/Attaque_de_l%27homme_du_milieu), [Transporte Layer Security](https://fr.wikipedia.org/wiki/Transport_Layer_Security), [masque jetable](https://fr.wikipedia.org/wiki/Masque_jetable), [Advanced Encryption Standard](https://fr.wikipedia.org/wiki/Advanced_Encryption_Standard) - Livre *Numérique et Sciences Informatiques, 24 leçons, Terminale*, T. BALABONSKI, S. CONCHON, J.-C. FILLIATRE, K. NGUYEN, éditions ELLIPSES. - Livre *Prépabac NSI, Terminale*, G. CONNAN, V. PETROV, G. ROZSAVOLGYI, L. SIGNAC, éditions HATIER. - Les schémas ont été réalisés avec des images libres de droit (uniquement Public Domain ou CC0) accessibles sur le site : [https://www.svgrepo.com/](https://www.svgrepo.com/). --- Germain Becker, Lycée Emmanuel Mounier, Angers.