Abrégé kppv en français. En anglais, on dit k nearest neighbors souvent abrégé knn.
L’algorithme des k plus proches voisins appartient à la famille des algorithmes d’apprentissage automatique (machine learning) qui constituent le poumon de l'intelligence artificielle actuellement.
Pour simplifier, l'apprentissage automatique part souvent de données (data) et essaye de dire quelque chose des données qui n'ont pas encore été vues : il s'agit de généraliser, de prédire.
Exemple d'introduction

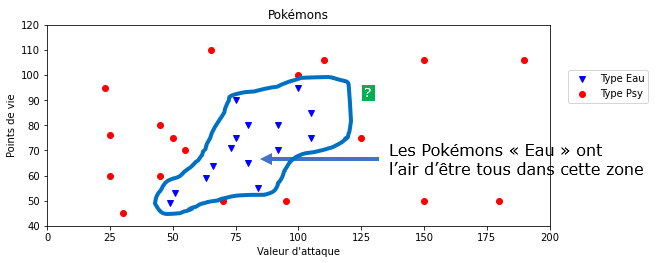
On dispose de données sur 34 Pokémons : leur type (Psy ou Eau), leur points de vie et la valeur de leurs attaques. On peut représenter ces données graphiquement, avec les points de vie en abscisses et les valeurs d'attaque en ordonnées.
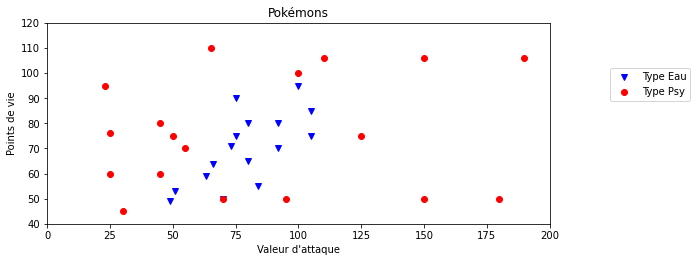
Les Pokémons de type "Eau" sont représentés pas les points bleus, et ceux de type "Psy" par les points rouges.
Peut-on prédire le type d'un nouveau Pokemon inconnu ?

Ce problème, qui demande à prédire à quelle catégorie, ou classe, appartient ce nouvel élément donné, est appelé problème de classification. L'algorithme des k plus proches voisins permet de trouver les k voisins les plus proches (si k = 5 on cherche les 5 voisins les plus proches) de ce nouvel élément dans le but de lui associer une classe plausible (Psy ou Eau, dans cet exemple).
A partir d'un jeu de données (par exemple, les données sur nos 34 Pokémons) et d'une donnée cible (le nouveau Pokemon à classifier), l'algorithme de $k$ plus proches voisins déterminer les $k$ données les plus proches de la cible.
Voici un algorithme permettant de résoudre ce problème :
Données et préconditions :
donnees de taille n contenant les données et leurs classesciblek inférieur à nRésultat : un tableau contenant les k plus proches voisins de la donnée cible.
Algorithme des kppv
distances_voisins contenant les éléments de la table donnees et leurs distances avec la donnée cible.distances_voisins selon la distance croissante avec la donnée cible.k premiers éléments de cette table triée.
L'algorithmes des kppv en lui-même n'apporte pas la réponse à notre problème de classification puisqu'il ne fournit que les k plus proches voisins (et leurs classes) de notre donnée cible. Il reste donc une dernière étape pour prédire la classe de notre nouvel élément : pour cela, on choisit la classe majoritaire (la plus présente) dans les k plus proches voisins.
On est contents si k est impair car il ne peut pas y avoir d'ex-aequo !
La valeur de $k$ est très importante, elle doit être choisie judicieusement car elle a une influence forte sur la prédiction. Regardons le résultat de la prédiction pour différentes valeurs de $k$ sur notre exemple.
Exemple 1 : le 1 plus proche voisin
Si $k = 1$, cela revient à chercher la donnée la plus proche de notre élément cible. Ici, on se rend compte que sa classe est "Psy" (point rouge) donc on classerait le nouveau Pokémon comme étant de type "Psy".
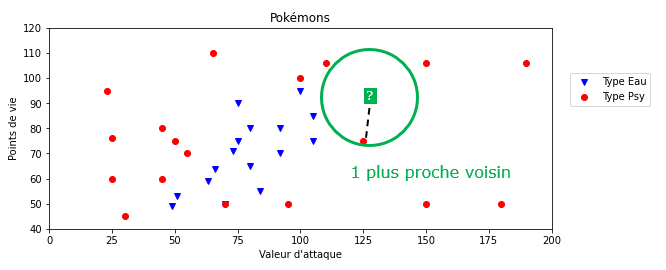
Exemple 2 : les 5 plus proches voisins
On se rend compte que la classe majoritaire dans les 5 plus proches voisins est "Psy" (3 points rouges contre 2 points bleus) donc on classerait le Pokemon inconnu comme étant de type "Psy".

Exemple 3 : les 9 plus proches voisins
On se rend compte que la classe majoritaire dans les 9 plus proches voisins est "Eau" (5 points bleus contre 4 points rouges) donc on classerait le Pokemon inconnu comme étant de type "Eau".
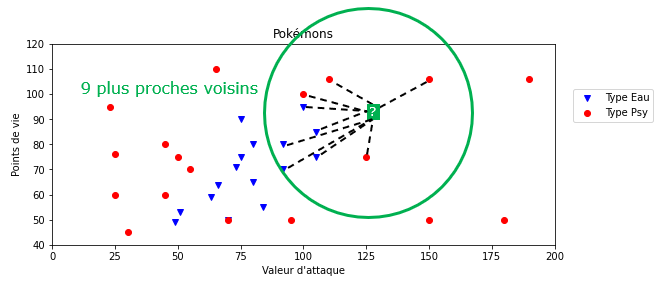
En poursuivant, si on choisit $k=34$ (le nombre total de données), alors la prédiction serait toujours "Psy" car c'est la classe majoritaire de l'échantillon. Il est donc incorrect de pense que plus la valeur de $k$ augmente meilleure sera la prédiction, c'est plus complexe que cela.
C'est bien beau tout ça, mais quelle valeur de $k$ faut-il choisir ?
Pour trouver une bonne valeur de $k$ il est possible d'appliquer le protocole expérimental suivant :
En appliquant ce protocole à différentes valeurs de $k$, on peut déterminer quelle valeur fournit les meilleurs résultats. Il est même judicieux de recommencer en retirant d'autres données pour affiner encore davantage la recherche de la meilleure valeur $k$ : on parle alors de validation croisée qui est une méthode d'apprentissage.
L'algorithme des plus proches voisins repose presque entièrement sur la distance entre deux données. Dans les exemples vus précédemment, c'est la distance "naturelle" qui a été choisie (celle "à vol d'oiseau").
Dans un repère orthonormé, si $A$ et $B$ ont pour coordonnées respectives $(x_A, y_A)$ et $(x_B, y_B)$ alors la distance entre ces deux points est donnée par la formule :
$$\text{distance}(A, B) = \sqrt{(x_B-x_A)^2 + (y_B-y_A)^2}.$$
On parle alors de la distance euclidienne. Sachez cependant qu'il existe d'autres distances et vous en rencontrerez dans les exercices. Par exemple, on peut très bien imaginer que les valeurs sur l'axe des ordonnées ne nous intéressent pas et utiliser une distance ne prenant en compte que l'axe des abscisses avec la formule $\text{distance}(A, B) = |x_B-x_A|$. Ainsi, sur notre exemple, et avec cette distance, la classe majoritaire des 9 plus proches voisins de notre nouveau Pokémon est "Psy" (6 points rouges contre 3 points bleus), ce qui donnerait une prédiction contraire à celle donnée en utilisant la distance "naturelle" (euclidienne).
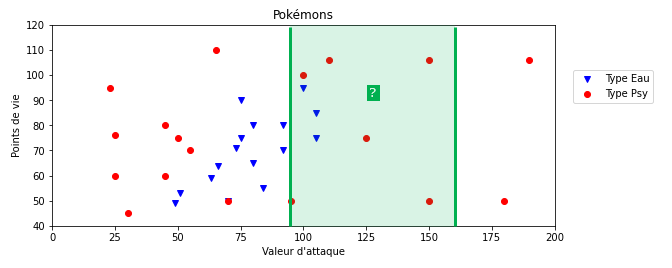
Moralité : On voit donc que le choix de la distance n'est pas anodin et que ce choix peut aboutir à des prédictions différentes.
Nous n'avons parlé ici que de distances géométriques qui ne s'appliquent qu'à des données chiffrées. Toutes les données ne sont pas adaptées à ce type de distance : si on veut comparer la distance entre deux chaînes de caractères (dans le but de prédire la langue d'origine de certains mots par exemple) d'autres types de distances sont à considérer : la distance de Hamming ou la distance d'édition qui seront abordées en Terminale.
La plupart des algorithmes d'apprentissage automatique cherchent à apprendre quelque chose du jeu de données qui lui est fourni, c'est-à-dire à remplacer les données par un modèle (une sorte de "règle" permettant de classer les données, de prendre une décision, etc.). Autrement dit, un tel algorithme tente de "comprendre" les données pour en déduire un modèle, on peut voir cela comme un apprentissage intelligent.
Pour illustrer cela de manière simplifiée, un algorithme d'apprentissage automatique intelligent chercherait par exemple, à partir des données, à délimiter deux "zones" séparant les Pokémons "Psy" des Pokémons "Eau". Il n'aurait alors plus besoin des données (des points) pour prédire la classe d'un nouvel élément car il suffirait de regarder dans quelle zone celui-ci se trouve (d'utiliser le modèle qu'il a deviné).
L'algorithme des k plus proches voisins n'a pas cette "intelligence" car il n'essaie pas de construire un modèle mais se sert des données elles-mêmes pour donner un résultat : on parle alors d'apprentissage par coeur.
L'algorithme des k plus proches voisins est-il alors un algorithme d'intelligence artificielle ?
L'apprentissage par coeur est clairement l'apprentissage le moins intelligent mais la réponse est OUI si on considère sa capacité de prédiction : classifier un élément qu'il n'a jamais vu.
Le deep learning (ou apprentissage profond) est une famille de méthode d'apprentissage automatique. En 2012, les techniques de deep learning ont réussi à fonctionner et obtenir des résultats spectaculaires. Ces résultats ont été rendus possibles notamment par l'arrivée de données en volume massifs (big data) permettant aux algorithmes d'apprendre à résoudre un problème. Ces données en masse permettent de disposer d'une importante quantité de données sur lesquelles entrainer et affiner les algorithmes.
Les stratégies mises en place par les géants du numérique (GAFAM) tournent entièrement autour de la récolte de données de leurs clients sur n'importe quel sujet pour "nourrir" leurs algorithmes d'apprentissage. C'est ainsi qu'Amazon arrive à nous proposer des "suggestions d'achat". Google quant à lui nous utilise lorsque nous devons prouver que nous ne sommes pas un robot. En effet, qui n'a pas déjà vu un écran de ce genre ?

En cliquant aux bons endroits, on assigne une classe aux différentes parties de l'image (feu de circulation ou non) et celles-ci viennent alimenter les bases de données sur lesquelles les algorithmes s'entraînent. Ils serviront ensuite aux voitures autonomes de Google à repérer les feux tricolores sur la route.
La qualité des données est primordiale dans l'apprentissage automatique car ce sont elles qui définissent presque entièrement la qualité des résultats des algorithmes. Voici quelques exemples, en vrac :
Your system is only as good as the data that you use to train it on,
Kate Crawford, cofounder and co-director of AI Now
Références :
Germain BECKER, Lycée Mounier, ANGERS 
Voir en ligne : info-mounier.fr/premiere_nsi/algorithmique/algorithme-kppv