Recherche dichotomique

On a déjà écrit un algorithme pour rechercher un élément dans un tableau. Cet algorithme de recherche séquentielle consistait à parcourir tous les éléments du tableau, un à un, jusqu'à trouver l'élément recherché ou arriver au bout du tableau sans le trouver :

def recherche_sequentielle(v, T):
    """Renvoie True si v appartient au tableau T, False sinon."""
    for elt in T:
        if elt == v:
            return True
    return False

Cet algorithme avait un coût de l'ordre de la taille $n$ du tableau, on parle de coût linéaire.

Peut-on faire mieux ? Oui, à condition que le tableau soit trié !

Ceci n'est qu'un résumé de cours et ne remplace en rien l'étude de l'algorithme qui a été faite dans l'activité et dans les exercices.

Algorithme de recherche dichotomique

Spécification

On cherche à écrire une fonction recherche_dichotomique(v, T) qui recherche une valeur v dans un tableau trié T dont voici la spécification :

Entrée(s) : un tableau T de taille $n$ constitué d'entiers, un entier v
Sortie(s) : un booléen
Rôle : renvoyer Vrai si $v\in T$, Faux sinon
Précondition(s) : T est trié par ordre croissant
Postcondition(s) : $\emptyset$

On pourrait écrire une fonction qui ne se contente pas de renvoyer Vrai ou Faux pour indiquer que la valeur v est trouvée ou non, mais de renvoyer une position de la valeur cherchée (et None si v n’est pas dans T). Il n’y aurait quasiment rien à modifier !

Idée de l'algorithme

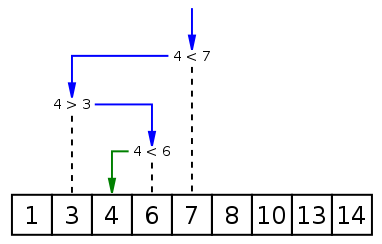
illustration de la recherche dichotomique

Recherche dichotomique dans un tableau trié.
Tushe2000, Public domain, via Wikimedia Commons

Idée de l'algorithme de recherche dichotomique :

Trouver la position la plus centrale du tableau (si le tableau est vide, sortir et renvoyer Faux)
Comparer la valeur de cette case à l'élément recherché v. Trois cas se présentent :
- Si v est égale à la valeur centrale, alors renvoyer Vrai
- Si v est strictement inférieure à la valeur centrale, alors reprendre la procédure dans la moitié gauche du tableau
- Si v est strictement supérieure à la valeur centrale, alors reprendre la procédure dans la moitié droite du tableau

Écriture de l'algorithme

Implémentation en Python

def recherche_dichotomique(v, T):
    """
    T : tableau d’entiers trié dans l’ordre croissant
    v : nombre entier
    La fonction renvoie True si T contient v et False sinon
    """
    debut = 0
    fin = len(T) - 1
    while debut <= fin:
        m = (debut + fin) // 2
        if v == T[m]:
            return True  # ou return m (pour renvoyer une position)
        if v > T[m]:
            debut = m + 1
        else:
            fin = m - 1
    return False  # ou return None (si on cherche à renvoyer une position)

>>> recherche_dichotomique(32, [2, 3, 9, 10, 16, 30, 32, 37, 50, 89])
True
>>> recherche_dichotomique(20, [2, 3, 9, 10, 16, 30, 32, 37, 50, 89])
False

Explications :

On note debut et fin les indices définissant la zone de recherche de v dans le tableau T. Au départ, on a donc debut = 0 et fin = len(T) - 1 :

Après un certain nombre d’étapes, on se trouve dans la situation suivante :

Le programme doit répéter ce principe de dichotomie tant que la zone de recherche n’est pas vide, donc tant que debut ≤ fin. L’utilisation d’une boucle « tant que » est toute indiquée !

while debut <= fin:

Il faut, à chaque étape, comparer l’élément v avec l’élément central de la zone de recherche. On va noter milieu l’indice de l’élément central. On a la situation suivante :

Pour calculer la position centrale m, il suffit de faire la moyenne entière de debut et fin :

m = (debut + fin) // 2

Il reste ensuite à comparer v avec T[m]. Trois cas de figure se présentent selon que v soit plus petite, plus grande ou égale à T[m] :

si v est égale à T[m] c’est qu’on a trouvé la valeur v en position m, il suffit de renvoyer ``.
si en revanche elle est plus grande, on se restreint à la moitié droite et on modifie la valeur de debut en conséquence :

if v > T[m]:
    debut = m + 1

sinon se restreint à la moitié gauche en modifiant la valeur de fin en conséquence :

else:
    fin = m - 1

Il se peut également qu’on finisse par sortir de la boucle car la condition debut <= fin devient fausse. Cela signifie que la valeur v ne se trouve pas dans T et dans ce cas on renvoie False.

Exemple

Recherche de la valeur v = 32 dans le tableau T = [2, 3, 9, 10, 16, 30, 32, 37, 50, 89] :

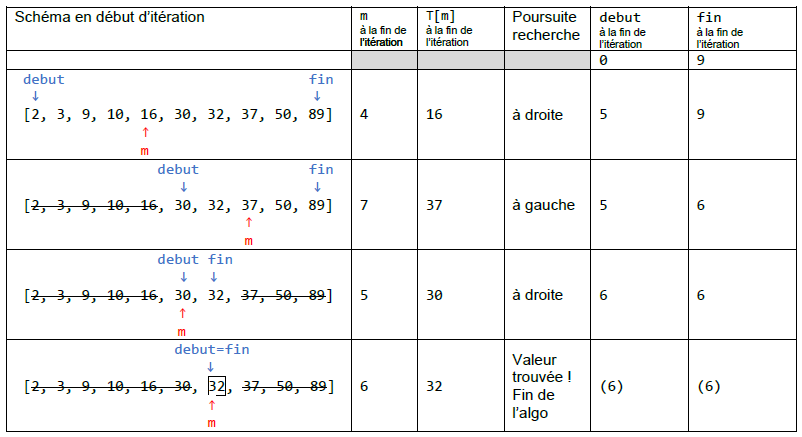
Il n'y a eu besoin d'examiner que 4 valeurs pour trouver la valeur recherché, alors qu'on aurait du en examiner 7 avec une recherche séquentielle.
Si on avait cherché la valeur 31, il n'y aurait eu que 4 valeurs à examiner également, mais 10 avec une recherche séquentielle.

Coût de l'algorithme

On peut mesurer expérimentalement l'efficacité de la recherche dichotomique en comparaison avec la recherche séquentielle.

Protocole expérimental

On va comparer le temps, dans le pire cas, pour chercher une valeur dans un tableau, selon l'algorithme de recherche séquentielle puis selon l'algorithme de recherche dichotomique.

Dans les deux cas, on se place dans le cas d'un tableau consitué uniquement de 0, qui est donc trié, et on y cherche la valeur 1 pour se placer dans un pire cas (une valeur absente du tableau). En raison, des fluctuations d'une mesure à l'autre, on a choisit d'effectuer 10 fois la recherche et de calculer le temps moyen.

Temps pour la recherche séquentielle

Voici le protocole de mesure et les résultats :

import time

def fabrique_tableau_de_zeros(taille):
    """Fabrication d'un tableau de zéros de taille `taille`."""
    return [0]*taille

def mesure_pire_cas_recherche_sequentielle(taille):
    """Mesure du temps dans le pire cas pour une recherche séquentielle."""

    # création du tableau (est long si taille est trop grand)
    tab = fabrique_tableau_de_zeros(taille)

    # mesure du temps pour la recherche sequentielle
    tps_total = 0
    for _ in range(10):
        t0 = time.time()
        recherche_sequentielle(1, tab)
        t1 = time.time()
        delta_t = t1 - t0
        tps_total = tps_total + delta_t
    tps_moyen = tps_total / 10

    print(f"Recherche séquentielle : temps pour un tableau de taille {taille} : {tps_moyen}")

>>> mesure_pire_cas_recherche_sequentielle(1000)
Recherche séquentielle : temps pour un tableau de taille 1000 : 0.00010001659393310547
>>> mesure_pire_cas_recherche_sequentielle(10000)
Recherche séquentielle : temps pour un tableau de taille 10000 : 0.000599980354309082
>>> mesure_pire_cas_recherche_sequentielle(10**5)
Recherche séquentielle : temps pour un tableau de taille 100000 : 0.00710000991821289
>>> mesure_pire_cas_recherche_sequentielle(10**6)
Recherche séquentielle : temps pour un tableau de taille 1000000 : 0.052099990844726565
>>> mesure_pire_cas_recherche_sequentielle(3*10**6)
Recherche séquentielle : temps pour un tableau de taille 3000000 : 0.1684999942779541

Analyse :

On constate que lorsqu'on multiplie la taille du tableau par $k$, le temps est aussi multiplié par un facteur d'environ $k$ : la recherche séquentielle a donc bien un coût linéaire.
Cela veut dire qu'il faudrait 1000 fois plus de temps pour la recherche dans un tableau de taille $10^9$ que dans un tableau de taille $10^6$ (car il est 1000 fois plus grand). En se basant sur le temps pour tableau de taille $10^6$, soit environ 0.05 sec, il faudrait donc $0,05 \times 1000 = 50$ sec pour la recherche dans un tableau de taille 1 milliard, ce qui est très long.

Temps pour la recherche dichotomique

Le protocole est exactement le même :

import time

def fabrique_tableau_de_zeros(taille):
    """Fabrication d'un tableau de zéros de taille `taille`."""
    return [0]*taille

def mesure_pire_cas_recherche_dichotomique(taille):
    """Mesure du temps dans le pire cas pour une recherche dichotomique."""

    # création du tableau (est long si taille est trop grand)
    tab = fabrique_tableau_de_zeros(taille)

    # mesure du temps pour la recherche dichotomique
    tps_total = 0
    for _ in range(10):
        t0 = time.time()
        recherche_dichotomique(1, tab)  # seule différence évidemment
        t1 = time.time()
        delta_t = t1 - t0
        tps_total = tps_total + delta_t
    tps_moyen = tps_total / 10

    print(f"Recherche dichotomique : temps pour un tableau de taille {taille} : {tps_moyen}")

>>> mesure_pire_cas_recherche_dichotomique(1000)
Recherche dichotomique : temps pour un tableau de taille 1000 : 0.0
>>> mesure_pire_cas_recherche_dichotomique(10000)
Recherche dichotomique : temps pour un tableau de taille 10000 : 0.0
>>> mesure_pire_cas_recherche_dichotomique(10**5)
Recherche dichotomique : temps pour un tableau de taille 100000 : 0.0
>>> mesure_pire_cas_recherche_dichotomique(10**6)
Recherche dichotomique : temps pour un tableau de taille 1000000 : 0.0

Sans surprise, la recherche dichotomique est quasi instantanée, même pour des tableaux très grands.

Efficacité de la recherche dichotomique

Comme toutes les opérations de l'algorithme sont élémentaires, déterminer son coût revient à compter le nombre d'itérations de la boucle while, c'est-à-dire le nombre de valeurs du tableau qui ont été examinées.

Comme à chaque étape, la zone de recherche est divisée par 2, le nombre de valeurs à examiner est toujours très petit.

Par exemple, en partant d'un million, il suffit de diviser 20 fois successivement par 2 pour obtenir un nombre inférieur ou égal à 1 (car $\frac{10^6}{2^{19}}>1$ et $\frac{10^6}{2^{20}}\leqslant 1$ ). Autrement dit, chercher dans un tableau d'un million de valeurs nécessite au maximum 20 étapes pour que la zone de recherche soit réduite à une seule valeur : il n'y a donc que 20 valeurs à examiner dans le pire cas (contre 1 million pour une recherche séquentielle).

De même, rechercher par dichotomie dans un tableau de taille 1 milliard, ne nécessite qu'au pire 30 étapes ($\frac{10^9}{2^{29}}>1$ et $\frac{10^9}{2^{29}}\leqslant 1$).

Coût logarithmique (hors programme)

L'algorithme de recherche dichotomique a un coût logarithmique, c'est-à-dire qu'il est de l'ordre de $\log_2(n)$ (on dit logarithme en base 2 de $n$ ou logarithme binaire de $n$).

Un coût logarithmique est bien meilleur qu'un coût linéaire puisque le nombre d'opérations est peu sensible à la taille du tableau d'entrée. Cela fait de l'algorithme de recherche dichotomique un algorithme très efficace.

Ce n'est pas au programme car cela fait appel aux fonctions logarithmes qui n'ont pas été étudiées en cours de mathématiques. Mais on donne ci-dessous la définition des informaticiens de ce que représente le logarithme binaire de n, pour que vous puissiez comprendre l'idée.

Pour les informaticiens, le logarithme binaire de $n$, noté $\log_2(n)$, est une valeur approchée (à 1 près) du nombre de fois qu'il faut diviser $n$ par $2$ pour obtenir un nombre inférieur ou égal à 1. À ce titre, vous pouvez aussi retenir que $\log_2(n)$ est égal, à 1 près, au nombre de bits qu'il faut pour écrire $n$ en binaire (en effet, lorsqu'on convertit $n$ en binaire, on effectue des divisions par deux jusqu'à ce que le reste soit égal à 0).

Sur votre calculatrice, vous pouvez aussi obtenir la valeur de $\log_2(n)$ en grâce à la fonction logarithme népérien (étudiée en spécialité Mathématiques en Terminale) qui est accessible via la touche "ln". En effet, pour tout réel $x>0$, on a : $\log_2(x) = \dfrac{\ln(x)}{\ln(2)}$.

Par exemple, $\log_2(10^6) = \dfrac{\ln(10^6)}{\ln(2)} \simeq 19,93$ et $\log_2(10^9) = \dfrac{\ln(10^9)}{\ln(2)} \simeq 29,90$ et on retrouve respectivement les 20 et 30 étapes nécessaires pour chercher par dichotomie une valeur dans un tableau d'un million et d'un milliard de valeurs.

Recherche séquentielle vs. dichotomique

Chercher une valeur par dichotomie est beaucoup plus efficace que d'effectuer une recherche séquentielle, mais nécessite que le tableau soit au préalable trié.

On peut se demander s'il n'est pas intéressant de trier initialement le tableau pour ensuite rechercher par dichotomie la présence de valeurs. En réalité, le tri est coûteux ! Les meilleurs algorithmes de tris sont plus coûteux qu'une recherche séquentielle dont le coût est linéaire. C'est donc plus coûteux de trier puis de rechercher par dichotomie que de chercher directement dans le tableau non trié de manière séquentielle.

En revanche, lorsque l'on sait que l'on a beaucoup de valeurs à chercher, cela peut devenir intéressant de trier le tableau une fois pour toutes au départ, puisque chaque recherche sera alors instantanée.

Terminaison de l'algorithme

Il nous reste à justifier pourquoi cet algorithme termine nécessairement (qu’il ne « tourne » pas à l’infini). On appelle cela : « prouver la terminaison de l’algorithme ».

Traitons tout de suite le cas où T est un tableau vide. Dans ce cas, debut = 0 et fin = -1 et donc debut > fin donc on n’entre pas dans la boucle while et donc l’algorithme termine (la fonction renvoie la valeur False directement).

Montrons que l’algorithme termine également si T n’est pas vide. Il faut donc montrer que la boucle while termine. Pour cela on va considérer la quantité fin – debut.

Dans notre cas, la quantité fin - debut s'appelle un variant de boucle. On va l'utiliser pour prouver la terminaison.

La quantité fin – debut est toujours un nombre entier au cours de l’algorithme (car debut et fin le sont).
Au départ, fin – debut est positive et on entre dans la boucle while
À chaque itération de la boucle while, trois cas se présentent :
- Soit la valeur v est trouvée et le return termine l’algorithme
- Soit fin diminue d’au moins une unité (instruction fin = m – 1) et donc fin – debut également ;
- Soit debut augmente au moins d’une unité (instruction debut = m + 1) et donc fin – debut diminue au moins d'une unité.

Ainsi, on sait que la quantité fin – debut est un nombre entier qui diminue strictement à chaque itération donc cette quantité deviendra forcément strictement négative donc on finira par avoir debut > fin et donc par sortir de la boucle while, si on n’a pas trouvé la valeur v avant bien sûr.

Pour prouver la terminaison d'une boucle while (une boucle for termine dans tous les cas), on utilise toujours un variant de boucle. C’est une quantité entière qui diminue strictement à chaque itération et qui reste positive. Le variant ne peut donc prendre qu’un nombre fini de valeurs, ce qui prouve que le nombre d’itérations de la répétitive « tant que » est fini, donc que celle-ci termine.

Bilan

La recherche dichotomique permet de rechercher une valeur dans un tableau trié.
Le principe consiste à couper en deux à chaque fois la portion du tableau dans laquelle s’effectue la recherche.
Cet algorithme est très efficace. Il ne faut que quelques dizaines de comparaisons pour chercher une valeur dans un tableau en contenant des milliards.
Pour l'appliquer, il faut que le tableau soit initialement trié, ce qui est une opération plus coûteuse que de rechercher directement de manière séquentielle dans le tableau non trié. Mais si on sait qu'il y a beaucoup de recherches à effectuer, cela peut valoir la peine de perdre un peu de temps au départ pour trier le tableau, puisque chaque recherche ultérieure sera quasiment instantanée si on procède par dichotomie.

Références :

Documents ressources de l'équipe éducative du DIU EIL, Université de Nantes, Christophe JERMANN et Christophe DECLERCQ.
Livre Numérique et Sciences Informatiques, niveau Première, T. BALABONSKI, S. CONCHON, J.-C. FILLIATRE, K. NGUYEN, éditions Ellipses
Cours de Gilles Lassus sur les dictionnaires (programme de Terminale) pour l'idée du protocole de mesure du temps.

Germain BECKER & Sébastien POINT, Lycée Mounier, ANGERS Licence Creative Commons

Recherche dichotomique [RÉSUMÉ]