Représentation binaire des entiers positifs

Introduction : analogie avec la base 10

Nous utilisons tous les jours la base 10 pour compter, c'est la base décimale. Par exemple, le nombre 4097 représente 4 milliers, 0 centaine, 9 dizaines et 7 unités.

$4097 = 4\times 1000 + 0 \times 100 + 9 \times 10 + 7 \times 1$ c'est-à-dire : $4097 = \textbf 4 \times 10^3 + \textbf 0\times 10^2 + \textbf 9 \times 10^1 + \textbf 7 \times 10^0$

On retrouve les chiffres $4$, $0$, $9$ et $7$ dans cette écriture avec des puissances de 10. On peut schématiser cela ainsi :

En base 10, chaque chiffre peut prendre 10 valeurs : de $0$ à $9$.

Comment ajouter 1 en base 10 ?

Vous le faites intuitivement, mais analysons ce qui se passe avec les chiffres de la représentation décimale. Il faudra faire exactement la même chose en base 2.

On regarde le chiffre des unités : s'il n'est pas au maximum ($\neq 9$) on lui ajoute $1$ ; s'il est au maximum, on le met à zéro et on regarde si on peut ajouter 1 au chiffre des dizaines, et ainsi de suite.

Voyons quelques exemples pour fixer les idées :

• On veut ajouter $1$ à $27$ : comme le chiffre des unités vaut $7$ ($\neq 9$) on lui ajoute directement $1$. On obtient donc $28$ ;
• On veut ajouter $1$ à $29$ : comme le chiffre des unités est à sa valeur maximale, on le met à $0$ et on regarde le chiffre des dizaines : il n'est pas à sa valeur maximale, on peut donc lui ajouter $1$. On obtient donc $30$.
• On veut ajouter $1$ à $99$ : comme le chiffre des unités vaut $9$ on le met à $0$ et on passe au chiffre des dizaines; celui-ci vaut aussi $9$ donc on le met aussi à $0$ et on passe au chiffre des centaines; celui-ci vaut $0$ donc on peut lui ajouter $1$. On obtient donc $100$.

Codage en base 2

Toute machine informatique, en raison de son architecture (cf. Thème 5, chapitres 1 et 2), ne manipule que des données exprimées en langage binaire, dans lequel tous les "mots" s'écrivent uniquement avec des 0 et des 1.

Dans la suite, on va voir comment on peut représenter un entier positif uniquement avec des 0 et des 1.

Tout cela est un peu pénible, et heureusement que je ne vous ai pas demandé de convertir 2022 en binaire... Il y a bien entendu une méthode pour convertir un nombre décimal en binaire.

Algorithme de conversion en binaire par suite de divisions

En divisant le nombre par 2, on obtient comme premier reste, le nombre d'unités. Si on recommence, on obtient les chiffres suivants de l'écriture en base 2. On s'arrête lorsque le quotient vaut 0.

Exemple : conversion de 42 en base 2

Méthode 1 : divisions successives par 2 (en ligne)

$$\begin{aligned} 42 &= 2\times 21 + {\color{red} \mathbf{0}} \newline 21 &= 2 \times 10 + {\color{red} \mathbf{1}} \newline 10 &= 2 \times 5 + {\color{red} \mathbf{1}} \newline 5 &= 2 \times 2 + {\color{red} \mathbf{0}} \newline 2 &= 2 \times 1 + {\color{red} \mathbf{1}} \newline 1 &= 2 \times 0 + {\color{red} \mathbf{0}} \end{aligned}$$

On obtient la valeur binaire en concaténant les restes obtenus du dernier au premier : $42 = (101010)_2$

Méthode 2 : divisions successives par 2 (divisions posées)

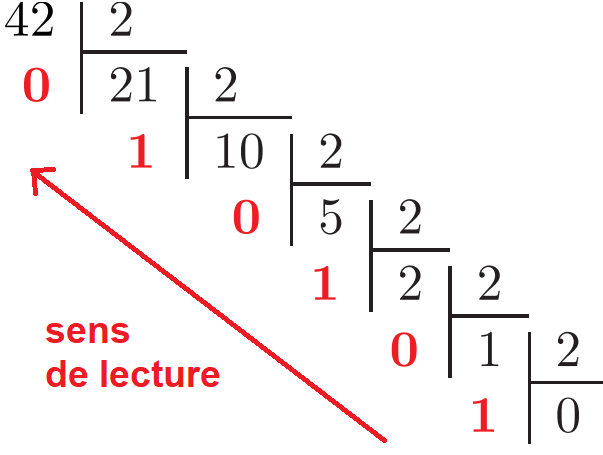
On obtient la valeur binaire en concaténant les restes obtenus du dernier au premier : $42 = (101010)_2$

Méthode 3 : Somme de puissances de 2

Les puissances de 2 sont : 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024, 2048, etc. On peut trouver la plus grande puissance de 2 inférieure ou égale au nombre décimal à convertir. La plus grande puissance de 2 inférieure ou égale à 42 est 32. Il manque alors 10 pour faire 42, donc on recommence avec 10 en cherchant la plus grande puissance de 2 inférieure ou égale à 10, etc :

$$\begin{align} 42 &= 32 + (10) \newline &= 32 + 8 + (2) \newline &= 32 + 8 + 2 \newline &= 2^5 + 2^3 + 2^1 \newline &= \mathbf{\color{red} 1} \times 2^5 + \mathbf{\color{red} 0} \times 2^4 + \mathbf{\color{red} 1} \times 2^3 + \mathbf{\color{red} 0} \times 2^2 + \mathbf{\color{red} 1} \times 2^1 + \mathbf{\color{red} 0} \times 2^0 \end{align}$$

Donc $42 = (101010)_2$.

En Python

On peut calculer l'écriture en binaire d'un entier avec la fonction Python bin().

>>> bin(42)
'0b101010'

Conversion binaire → décimale

La conversion binaire vers décimale est plus simple.

De la même manière que les chiffres de l'écriture décimale représentent des puissances de 10, les chiffres de l'écriture binaire représentent des puissances de 2.

Prenons l'exemple du nombre binaire $11010111$ :

Ainsi, pour convertir $(11010111)_2$ en décimal, on multiplie le premier chiffre (celui de droite) par $2^0$, le second par $2^1$, le troisième par $2^2$, etc. On calcule ensuite la somme de ces valeurs pour obtenir le nombre en décimal.

On obtient : $$(11010111)_2 = \textbf 1 \times 2^0 + \textbf 1 \times 2^1 + \textbf 1 \times 2^2 + \textbf 0 \times 2^3 + \textbf 1 \times 2^4 + \textbf 0 \times 2^5 + \textbf 1 \times 2^6 + \textbf 1 \times 2^7$$ c'est-à-dire : $$(11010111)_2 = 1 + 2 + 4 + 0 + 16 + 0 + 64 + 128 = 215.$$

Attention à bien commencer par le chiffre des unités !

En Python

On peut utiliser la fonction int() pour convertir un nombre binaire en décimal :

>>> int('11010111', 2)  # le '2' pour indiquer que la chaine est en base 2
215

On peut aussi directement saisir un nombre en binaire en préfixant son écriture par 0b.

>>> 0b11010111
215

Dans les exercices, on écrira les algorithmes de conversion entre base 10 et base 2. On verra également comment additionner ou multiplier deux nombres binaires.

Codage en base 16

Cette base est appelée base hexadécimale (hexa = 6 + décimale = 10). Nous allons passer plus rapidement cette partie car les méthodes restent les mêmes qu'avec la base 2.

• En base 10 : chaque chiffre peut être codé par 10 valeurs ($0,1,2,3,4,5,6,7,8,9$).
• En base 2 : chaque chiffre peut être codé par 2 valeurs ($0,1$).
• En base 16 : sans surprise, chaque chiffre peut être codé par 16 valeurs ($0,1,2,3,4,5,6,7,8,9,...$ et après ?). Après le $9$, on va utiliser les lettres de l'alphabet pour arriver à 16 valeurs en tout.

Ainsi, en base 16, chaque "chiffre" est codé par : $0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F$ avec la correspondance suivante :

Pourquoi la base 16 ?

L'avantage de la base 16 réside dans sa facilité de conversion de et vers la base 2. Un chiffre en base 16 remplace 4 bits (chiffres en base 2). Elle est donc un compromis entre le code binaire des machines et une base de numération pratique à utiliser pour les ingénieurs.

L'hexadécimal a été utilisé la première fois en 1956 par les ingénieurs de l'ordinateur Bendix G-15. Pour plus d'informations sur le système hexadécimal : Système hexadécimal - Wikipédia.

Conversion en hexadécimal

L'algorithme est exactement le même que pour la conversion en binaire. Il suffit juste de diviser successivement par 16 et non par 2.

Exemple : conversion de 215 en base 16

Méthode 1

215 = 16 $\times$ 13 + 7
13 = 16 $\times$ 0 + 13 (→ D)

On obtient la valeur hexadécimale en concaténant les restes obtenus du dernier au premier : $215 = (D7)_{16}$

Méthode 2

On obtient la valeur hexadécimale en concaténant les restes obtenus du dernier au premier : $215 = (D7)_{16}$

La troisième méthode est possible mais est beaucoup moins adaptée car il faut connaître les puissances de 16.

En Python

On peut calculer l'écriture en binaire d'un entier avec la fonction Python hex().

>>> hex(215)
'0xd7'

Pourquoi la base 16 ? (bis)

Conversion hexadécimale → décimale

Le principe est le même que la conversion binaire vers décimale.

Plutôt qu'un long discours, un exemple :

Exemple : conversion de $(4E8)_{16}$ en base 10 :

Donc : $(4E8)_{16}=8\times 16^0 + E\times 16^1 + 4 \times 16^2 = 8 \times 1 + 14 \times 16 + 4 \times 256 = 8 + 224 + 1024 = 1256$.

En Python

On peut utiliser la fonction int() pour convertir une valeur hexadécimale en décimal :

>>> int('4e8', 16)  # on précise bien que la base d'origine est la base 16
1256

On peut aussi directement saisir un nombre en hexadécimal en préfixant son écriture par 0x.

>>> 0x4e8
1256

Ecriture d'un entier positif dans une base $b\geq 2$ quelconque

Généralisation

Dans une base $b\geq 2$ quelconque, on procède exactement de la même façon mais avec des puissances de $b$ !

Exemple : écriture de l'entier 38 en base 5

$$38 = \textbf 1 \times 5^2 + \textbf 2 \times 5^1 + \textbf 3 \times 5^0.$$ Le nombre 38 s'écrit donc $(123)_5$ en base 5.

Écriture d’un entier positif dans une base $b \geq 2$ :

où les $a_i$ sont des chiffres entre 0 et $b-1$

On note cela :

Bilan

• L'écriture binaire, aussi appelée écriture en base 2, est similaire à l'écriture décimale (en base 10) que nous utilisons tous les jours, mais les nombre s'écrivent avec seulement 2 chiffres (0 et 1), et on doit raisonner en puissances de 2, en divisant par 2, etc.
• Comme une machine ne manipule que deux valeurs : 0 et 1, on dit qu'elle parle le langage binaire. Le bit est l'unité de base du langage est les mots de 8 bits sont appelés des octets.
• Les entiers (comme tout le reste) sont donc nécessairement écrits en binaire pour être manipulé par un ordinateur. On a vu comment passer de la base 10 à la base 2 (et réciproquement).
• La base hexadécimale (base 16) est aussi très utilisée en informatique car c'est un compromis intéressant entre la base 2 (compliquée à utiliser pour un humain) et la base 10 (utilisée facilement). Le passage en base 16 est similaire à celui en base 2, mais en raisonnant avec des puissances de 16, en divisant par 16, etc.
• On peut théoriquement définir une base $b \geq 2$ quelconque mais la maîtrise des bases 2 et 16 (et 10 !) est largement suffisante pour comprendre la manière dont sont représentées les informations en machine (ce que nous poursuivrons dans les chapitres suivants de ce thème).

Références :

• Équipe pédagogique du DIU EIL, université de Nantes.
• Cour de David Roche : https://pixees.fr/informatiquelycee/n_site/nsi_prem_base_2_16.html

Germain BECKER & Sébastien POINT, Lycée Mounier, ANGERS