Dans cette séance, on étudie comment un réseau social peut être modélisé mathématiquement. Cette modélisation permet de représenter les relations entre les personnes et il est alors possible d'appliquer toute sorte d'algorithmes : de recommandation, d'analyse de comportement, de calculs, etc.
Crédit : GDJ via Pixabay.
Soit un ensemble d’amis connectés sur un réseau social quelconque. Voici les interactions que l’on a recensées :
Pas facile de se représenter les liens qui existent entre eux, et encore il n'y a que 8 personnes, imaginez un réseau social de plusieurs millions d’abonnés 🤔 ! Essayons de représenter cela par un schéma, vous verrez c'est beaucoup plus parlant !
On va représenter le réseau social de la façon suivante :
Regardez la vidéo ci-dessous, du début à 3 min 37 s, puis répondez aux questions suivantes.
Source : https://youtu.be/YYv2R1cCTa0?end=217
Voici deux définitions importantes :
Exemple : Le graphe de notre réseau social est le suivant :
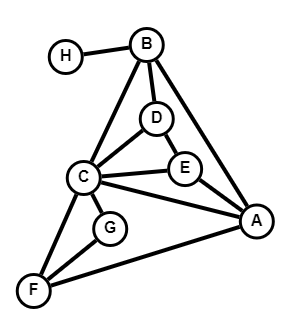
Pour aller du sommet A au sommet H, on peut prendre le chemin : A - E - C - B - H, soit un chemin passant par quatre arêtes. Mais il existe un chemin passant uniquement par deux arêtes : A - B - H. On ne peut pas faire plus court donc la distance entre les sommets A et H est égale à 2, on note cela $\text{distance}(A, H) = 2$.
Si on observe la distance entre le sommet A et chacun des autres sommets du graphe, on obtient les distances suivantes : $\text{distance}(A,A) = 0$ , $\text{distance}(A,B) = 1$ , $\text{distance}(A,C) = 1$ , $\text{distance}(A,D) = 2$ , $\text{distance}(A,E) = 1$ , $\text{distance}(A,F) = 1$ , $\text{distance}(A,G) = 2$ et $\text{distance}(A,H) = 2$.
On constate que la distance maximale entre le sommet A et les autres sommets du graphe est égale à 2, donc l’écartement du sommet A est égal à 2.
On peut avantageusement s’aider d’un tableau pour reporter toutes les distances entre les sommets et en déduire l’écartement de chaque sommet. C’est ce qui est proposé ci-dessous.
| A | B | C | D | E | F | G | H | Écartement | |
|---|---|---|---|---|---|---|---|---|---|
| A | 0 | 1 | 1 | 2 | 1 | 1 | 2 | 2 | 2 |
| B | |||||||||
| C | |||||||||
| D | 2 | 1 | 1 | 0 | 1 | 2 | 2 | 2 | 2 |
| E | 1 | 2 | 1 | 1 | 0 | 2 | 2 | 3 | 3 |
| F | 1 | 2 | 1 | 2 | 2 | 0 | 1 | 3 | |
| G | |||||||||
| H | 2 | 1 | 2 | 2 | 3 | 3 | 3 | 0 |
Voici les définitions de ces trois notions :
On considère ici le graphe du réseau social de départ (Exercice 1).
En lisant attentivement les trois définitions données au-dessus, répondez aux questions suivantes. Aidez-vous du tableau construit précédemment dans l'exercice 3.
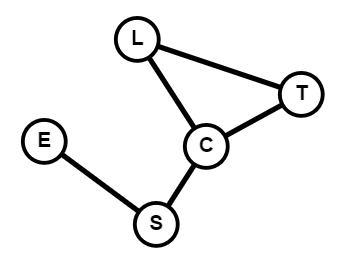
Voici un graphe représentant un autre réseau social.
On reprend le graphe de notre réseau social de départ. On peut aussi utiliser un tableau pour représenter ce graphe. Dans ce tableau, il suffit de mettre un “1” pour signifier une relation (d’amitié) et un “0” pour signifier une absence de relation entre deux personnes.
Cela donnerait le tableau suivant :
| A | B | C | D | E | F | G | H | |
|---|---|---|---|---|---|---|---|---|
| A | 0 | 1 | 1 | 0 | 1 | 1 | 0 | 0 |
| B | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
| C | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 |
| D | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 |
| E | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 |
| F | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 |
| G | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| H | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
Ce tableau est appelé tableau d’adjacence ou matrice d’adjacence du graphe. Il peut facilement être représenté dans la mémoire d’un ordinateur puisqu’il traduit le graphe par une série de “0” et de “1”.
On donne ci-dessous le tableau d’adjacence d’un graphe représentant un réseau social.
| Mick | Léa | Jade | Paul | Marc | |
|---|---|---|---|---|---|
| Mick | 0 | 1 | 1 | 0 | 0 |
| Léa | 1 | 0 | 1 | 0 | 1 |
| Jade | 1 | 1 | 0 | 1 | 1 |
| Paul | 0 | 0 | 1 | 0 | 0 |
| Marc | 0 | 1 | 1 | 0 | 0 |
Références :
Les enseignants du lycée Emmanuel Mounier à Angers 
Cette page en version PDF : T3_S3_Graphes.pdf
Voir en ligne : info-mounier.fr/snt/reseaux_sociaux/rs-graphes