La récursivité

Pochette de l'album Ummagumma de Pink Floyd.

Commençons par quelques définitions trouvées sur Wikipédia :

• Récursivité : démarche qui fait référence à l'objet même de la démarche à un moment du processus.
• Récursivité (programmation informatique) : Fait pour un objet de s'appeler lui-même.
• Un objet est dit récursif s'il se définit à partir de lui-même, s'il apparait dans sa définition.
• Une construction est récursive si elle se définit à partir d’elle-même.

Ainsi, les exemples suivants sont des cas concrets de récursivité :

• décrire un processus dépendant de données en faisant appel à ce même processus sur d'autres données plus « simples » ;
• montrer une image contenant des images similaires (comme la pochette de l'album Ummagumma de Pink Floyd ci-dessus) ;
• faire pointer un article de Wikipédia vers lui-même ou vers un article qui, par une succession de pointeurs, pointe vers l'article dont on est parti.

Retour sur les listes

Des constructions récursives

Une des opérations primitives du type abstrait Liste est le constructeur construit(e, L) qui crée une liste dont la tête est l'élément e et la queue est la liste L. Pour construire la liste formée par les nombres 5, 3, 8 et 1 il fallait procéder ainsi :

construit(5, construit(3, construit(8, construit(1, listevide()))))

Ceci est une construction récursive car l'opérateur construit s'appelle lui-même à plusieurs reprises. Dans le cas de notre implémentation avec des couples, cette construction mémorisait notre liste dans le tuple suivant :

(5, (3, (8, (1, None))))

Une première fonction récursive

Nous avions également défini l'opération dernier(L) qui doit renvoyer le dernier élément d'une liste L. Cette opération était implémentée par la fonction suivante :

def dernier(L):
    while reste(L) != listevide():  # tant que le reste de la liste n'est pas vide
        L = reste(L)  # on passe au reste
    return premier(L)  # on renvoie le premier élément de la dernière paire

Il s'agit d'une fonction écrite de manière itérative car elle ne s'appelle pas elle-même. On se propose d'écrire une version récursive de cette fonction. Il faut commencer par réfléchir un peu...

Comment obtenir le dernier élément d'une liste ?

C'est assez simple en fait :

• si le reste est la liste vide, on a trouvé le dernier élément
• sinon, le dernier élément de L est égal au dernier élément du reste de L : dernier(L) = dernier(reste(L)). En effet, si L est la liste de nombres 5, 2, 8, 1 alors :
  • dernier(L) vaut 1
  • reste(L) est la liste de nombres 2, 8, 1 qui a aussi pour dernier élément 1 donc dernier(reste(L)) vaut aussi 1.

On vient de voir que pour trouver le dernier élément d'une liste il suffit de calculer le dernier élément du reste de la liste, et répéter ce processus jusqu'à ce que le reste soit vide.

On ramène ainsi le calcul du dernier élément d'une liste au calcul du dernier élément d'une liste plus petite (reste(L)) jusqu'à ce que cela devienne impossible.

Illustration sur un exemple : pour calculer le dernier élément de la liste 5, 3, 8, 1 :

• on veut trouver dernier(5, 3, 8, 1)
• cela revient à calculer dernier(reste(5, 3, 8, 1)) c'est-à-dire dernier(3, 8, 1)
• qui est égal à dernier(reste(3, 8, 1)) c'est-à-dire dernier(8, 1)
• qui est égal à dernier(reste(8, 1)) c'est-à-dire dernier(1)
• qui est égal à 1 est on s'arrête ici puisque 1 n'a plus de reste. La réponse est donc 1 !

Bilan : On peut récrire la fonction dernier de manière récursive de la façon suivante :

def dernier(L):
    if reste(L) == listevide(): # si le reste est vide, c'est terminé
        return premier(L)       # et on renvoie alors sa tête
    else:
        return dernier(reste(L)) # sinon la réponse est le dernier élément du reste

Analyse : Cette fonction est bien récursive puisqu'elle s'appelle elle-même. On trouve ici le schéma classique d'un algorithme récursif :

• On définit le cas de base (ici lorsque le reste est vide) qui est un cas pour lequel on peut donner le résultat facilement. Il n'est alors plus nécessaire de faire un appel récursif donc cela constitue notre condition d'arrêt (sinon la fonction s'appellerait à l'infini) ;
• Sinon, on fait un appel récursif à la fonction mais sur une donnée plus petite (ici une liste plus petite).

Comme les appels récursifs se font sur des données dont la taille diminue, on est sûr d'aboutir (au bout d'un certain nombre d'appels) au cas de base qui mettra fin aux appels récursifs, ce qui assure la terminaison de l'algorithme.

La plupart des opérations sur les listes peuvent être implémentées par des fonctions récursives.

✏️ À faire : Exercice 1

Dérouler l'exécution d'une fonction récursive

Il est important de comprendre que chaque appel récursif met « en pause » l'exécution en cours, en attente d'obtenir le résultat qui est déterminé par l'appel suivant. Concrètement :

• Les appels sont tour à tour mis « en pause » jusqu'au dernier appel qui fourni un résultat. On appelle cela le dépliage (ou la descente).
• Ce résultat est ensuite transmis à l'appel précédent qui l'utilise pour calculer son propre résultat et le transmettre à l'appel précédent, et ainsi de suite jusqu'au premier appel qui peut alors calculer le résultat final. On appelle cela l'évaluation (ou la remontée).

Voici deux exemples qui illustrent ces deux étapes.

Exemple de la fonction dernier

Nous récrivons cette fonction pour l'avoir sous les yeux et déroulons l'exécution de l'appel dernier((5, (3, (8, None))).

def dernier(L):
    if reste(L) == listevide():
        return premier(L)
    else:
        return dernier(reste(L))

Phase de dépliage :

• 1er apppel : dernier((5, (3, (8, None)))
  • reste(L) = (3, (8, None))
  • ligne 5 : doit renvoyer la valeur dernier((3, (8, None))) qui nécessite un deuxième appel pour être évaluée. Le premier appel est donc mis en pause pour attendre le résultat du deuxième.
• 2ème appel : dernier((3, (8, None)))
  • reste(L) = (8, None)
  • ligne 5 : doit renvoyer la valeur dernier((8, None)) qui nécessite un troisième appel pour être évaluée. Le deuxième appel est donc mis en pause pour attendre le résultat du troisième.
• 3ème appel : dernier((8, None))
  • reste(L) = None
  • ligne 3 : renvoie le résultat 8 (puisque le reste est vide) qui est celui attendu par le deuxième appel.

Phase d'évaluation :

• 2ème appel (suite et fin) : Le deuxième appel attendait la valeur de dernier((8, None)) pour la renvoyer. Celle-ci a été évaluée à 8 par le troisième appel donc dernier((3, (8, None))) renvoie la valeur 8.
• 1er appel (suite et fin) : Le premier appel attendait la valeur de dernier((3, (8, None))) pour la renvoyer. Celle-ci a été évaluée à 8 par le second appel donc dernier((5, (3, (8, None))) renvoie la valeur 8 qui est le résultat final.

On peut résumer ces étapes par le schéma ci-dessous :

Fig. 1 - Déroulement des appels récursifs.

Autre exemple : calcul de puissances

On se propose d'écrire une fonction récursive (naïve) qui calcule les puissances de 2 c'est-à-dire une fonction deux_puissance(n) qui renvoie la valeur de $2^n$, où n est un entier positif.

Ecriture de la fonction récursive

Commençons par réfléchir à la façon dont on peut calculer $2^n$.

• Le cas de base correspond à $n=0$ et dans ce cas $2^n=2^0=1$.
• Sinon, on peut calculer $2^n$ en faisant $2 \times 2^{n-1}$.

On a désormais tout ce qu'il faut car on sait comment passer du calcul de $2^n$ à celui de $2^{n-1}$ pour notre appel récursif et on connaît le cas de base qui sera notre condition d'arrêt de la récursion :

Voici la fonction récursive que l'on peut écrire :

def deux_puissance(n):
    if n == 0:    # cas de base
        return 1
    else:         # sinon appel récursif avec un argument plus petit
        return 2 * deux_puissance(n-1)

>>> deux_puissance(3)
8

Déroulement de son exécution

Nous allons représenter de différentes (autres) manières l'exécution de deux_puissance(3).

Arbre d'appel

                        DEPLIAGE                                  |   EVALUTATION
                                                                  |
deux_puissance(3) = return 2 * deux_puissance(2)                  |   2 * 4 = 8
                                |                                 |     |
                          return 2 * deux_puissance(1)            |   2 * 2 = 4
                                        |                         |     |
                                     return 2 * deux_puissance(0) |   2 * 1 = 2 
                                                    |             |     |
                                                return 1          |     1

Autre représentation

deux_puissance(3)                          
-> 2 * deux_puissance(2)                -> DEPLIAGE
-> -> 2 * 2 * deux_puissance(1)          
-> -> -> 2 * 2 * 2 * deux_puissance(0)
.......................................................
<- <- <- 2 * 2 * 2 * 1                    
<- <- 2 * 2 * 2                         <- EVALUATION
<- 2 * 4                                 
8                                        

Autre représentation (bis)

deux_puissance(3)
    2 * deux_puissance(2) = ?
    appel à deux_puissance(2)
        2 * deux_puissance(1) = ?         DEPLIAGE
        appel à deux_puissance(1)
            2 * deux_puissance(0) = ?
            appel à deux_puissance(0)
......................................................
            renvoie 1
            2 * 1
        renvoie 2
        2 * 2                             EVALUATION
    renvoie 4
    2 * 4
renvoie 8

Empilement des appels

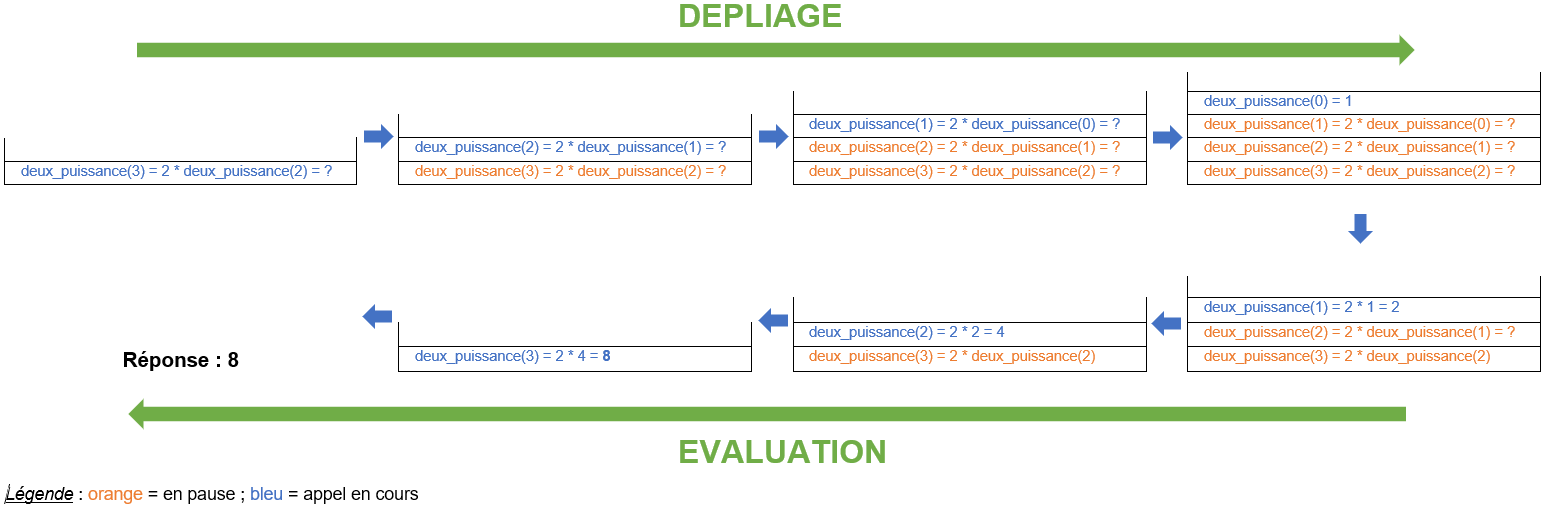
Fig. 2 - Pile d'exécution des appels récursifs.

Utilisation d'outils

On peut visualiser avec Python Tutor le dépliage (descente) puis l'évaluation (remontée) : lien vers pythontutor.

Mais le mieux est d'exécuter le programme avec l'environnement Thonny qui permet de voir en mode pas à pas les appels récursifs par ouverture d'une nouvelle fenêtre à chaque appel d'une fonction.

Logo du logiciel Thonny.
Crédits : Aivar Annamaa, MIT, via Wikimedia Commons

Récursif vs itératif

Il est prouvé que tout programme récursif peut être transformé en un programme impératif et réciproquement (même si ce n'est pas toujours évident).

Quel choix doit-on faire pour écrire un programme ?

Puissances de deux - version itérative

def deux_puissance_iter(n):
    reponse = 1
    for i in range(n):
        reponse = reponse * 2
    return reponse

Puissances de deux - version récursive

def deux_puissance_rec(n):
    if n == 0:
        return 1
    else:
        return 2 * deux_puissance_rec(n-1)

Une manière de penser

La façon de raisonner n'est pas la même selon la méthode :

• en itératif, on doit penser à la suite des ordres à appliquer pour progresser des données vers le résultat,
• en récursif, on commence par réfléchir à l'expression du résultat à calculer (dans le(s) cas de base et le cas récursif)

Ces deux méthodes de raisonnement sont respectivement à la base de la programmation impérative (que nous avons utilisé jusqu'à présent) et de la programmation fonctionnelle que nous étudierons cette année. En particulier, vous verrez que les fonctions récursives se traduisent très facilement en des fonctions respectant le paradigme de programmation fonctionnelle.

Une question d'élégance ?

Même si la méthode impérative nous est plus familière, il faut reconnaître que la méthode récursive est plus élégante, plus lisible et souvent plus courte à écrire car elle évite d'utiliser de nombreuses structures itératives.

De plus, la méthode récursive est très utile pour écrire des algorithmes sur des structures de données abstraites comme les listes, les arbres et les graphes. Elle est également souvent utilisée pour écrire des algorithmes de la catégorie « diviser pour régner ». Nous étudierons tout cela cette année.

Une question d'efficacité ?

En temps

Le modèle électronique d'un ordinateur est impératif, donc tout programme doit être complilé en itératif. Un programme récursif doit donc être dérécursivé (traduit en itératif) par le compilateur pour être exécuté. Cette phase de dérécursivation implique qu'un programme récursif s'exécute toujours (un peu) plus lentement qu'un programme itératif, mais l'ordre de grandeur est le même.

En espace

Nous avons vu que l'exécution d'un programme récursif entraînait des appels récursifs qui sont successivement mis en attente du résultat de l'appel suivant. Il est donc nécessaire de stocker en mémoire le contexte dans lequel chaque appel de la fonction a lieu (la valeur de ses paramètres, l'adresse mémoire de retour). En pratique, lors de la descente (phase de dépliage), ces contextes sont empilés au fur et à mesure les uns au-dessus des autres et sont dépilés au fur et à mesure lors de la remontée (phase d'évalution) comme sur le dernier schéma d'exécution.

L'environnement Thonny permet de bien visualiser cet empilement/dépilement des différents contextes d'appels.

Cet empilement (et dépilement) est assuré par une structure de données abstraite appelée pile que nous étudierons également cette année. Le dernier schéma proposé correspond à ce qu'on appelle la pile d'exécution de la fonction récursive. Cette pile est coûteuse en mémoire et rend les programmes récursifs plus coûteux en mémoire. De plus, cette pile n'a pas une taille infinie ce qui limite le nombre d'appels récursifs possibles : s'il y en a trop, la pile devient pleine et le programme terminera par une erreur.

Certains langages de programmation spécialisés dans l'écriture de programmes récursifs savent optimiser cela et ainsi éviter tout débordement de la pile. C'est le cas des langages fonctionnels (comme LISP) mais ce n'est le cas de Python.

En Python, le nombre d'appels récursifs est limité. Si on le dépasse, une erreur de type RecursionError est levée. On peut le voir facilement :

>>> deux_puissance_rec(3000)
Traceback (most recent call last):
...
RecursionError: maximum recursion depth exceeded in comparison

La version itérative renvoie le résultat :

deux_puissance_iter(3000)
>>> 1230231922161117176931558813276752514640713895736833715766118029160058800614672948775360067838593459582429649254051804908512884180898236823585082482065348331234959350355845017413023320111360666922624728239756880416434478315693675013413090757208690376793296658810662941824493488451726505303712916005346747908623702673480919353936813105736620402352744776903840477883651100322409301983488363802930540482487909763484098253940728685132044408863734754271212592471778643949486688511721051561970432780747454823776808464180697103083861812184348565522740195796682622205511845512080552010310050255801589349645928001133745474220715013683413907542779063759833876101354235184245096670042160720629411581502371248008430447184842098610320580417992206662247328722122088513643683907670360209162653670641130936997002170500675501374723998766005827579300723253474890612250135171889174899079911291512399773872178519018229989376

✏️ A faire : Activités 2, 3, 4 et 5

Bilan

• Un programme (une fonction ici) est dit récursif lorsqu'il s'appelle lui-même.
• La récursivité est avant tout un principe algorithmique de description de la solution d’un problème dont le principe consiste à ramener la résolution du problème à la résolution du même problème mais sur un objet plus petit. La méthode récursive est souvent plus élégante, concise et compréhensible que la méthode itérative.
• Pour écrire une fonction récursive il est nécessaire de penser récursif :
  • commencer par trouver le(s) cas de base dans le(s)quel(s) on peut donner une réponse au problème
  • déterminer ensuite l'expression des cas récursifs qui visent à trouver la réponse en fonction de la réponse au même problème mais sur des données de plus petite taille.
• L'exécution d'une fonction récursive se déroule en deux phases : la phase de dépliage (ou descente) et la phase d'évaluation (remontée). Dans la première, chaque appel récursif fait à son tour un appel récursif jusqu'au(x) cas de base qui termine(nt) cette cascade d'appels. Commence ensuite la deuxième phase où les évaluations (des résultats) remontent jusqu'à l'appel initial qui termine l'exécution.
• Dans la phase de descente, comme l'exécution de chaque appel est « mis en pause » au moment de l'appel récursif suivant, on mémorise leurs états (contextes) en les empilant dans une pile. Ils sont ensuite dépilés successivement lors de la remontée. Cet empilement est coûteux en mémoire et, en Python, il faut veiller à ne pas dépasser la capacité maximale de la pile.

Références :

• Documents ressources de l'équipe éducative du DIU EIL, Université de Nantes, Christophe JERMANN et Christophe DECLERCQ, licence CC BY-NC-SA.

Germain BECKER, Lycée Mounier, ANGERS

Ressource éducative libre distribuée sous Licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International