Un arbre est une structure hiérarchique permettant de représenter de manière symbolique des informations structurées.
Par exemple :
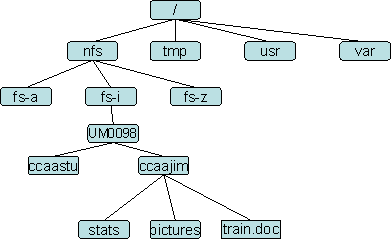
Crédits : Jimbotyson, CC BY-SA 3.0, via Wikimedia Commons.
Crédits : Ælfgar, CC BY-SA 3.0, via Wikimedia Commons
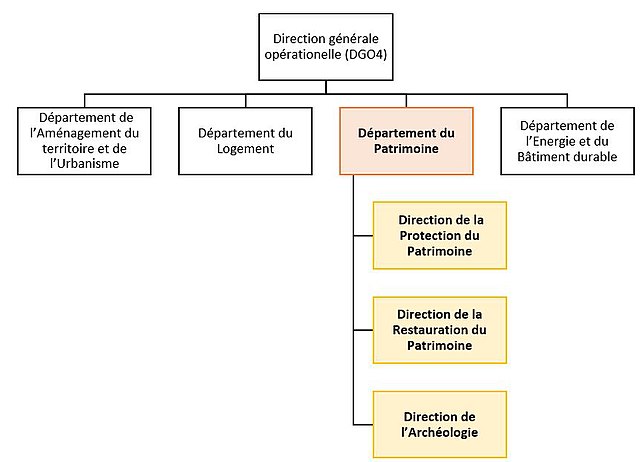
Crédits : Adriencld, CC BY-SA 4.0, via Wikimedia Commons
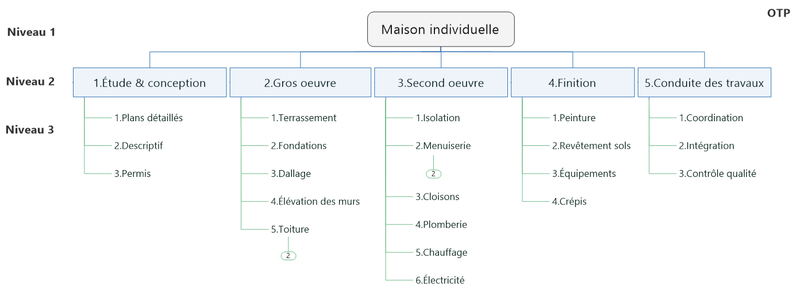
Crédits : Cth027, CC BY-SA 4.0, via Wikimedia Commons
Crédits : Birger Eriksson, CC BY-SA 3.0, via Wikimedia Commons
Dans le même ordre d'idée, le format JSON a également une structure arborescente.
Dans tous ces exemples, on a défini un cas où l'information est élémentaire (fichier, tâche élémentaire), et un cas général où l'information structurée contient deux ou plusieurs informations de même structure.
Dans la terminologie informatique, on utilise les termes de
Attention : l'analogie avec les arbres réels peut s'avérer trompeuse. Les arbres - en informatique - sont le plus souvent représentés avec la racine en haut, puis les noeuds, et les feuilles en bas.
Il s'agit d'une structure de données absraite permettant de représenter une collection de données par des noeuds organisés de manière hiérarchique : il y a un (parfois plusieurs) noeud racine et chaque noeud dépend d'un antécédent (sauf la racine) et a des descendants (sauf les feuilles).
Dans le vocabulaire des arbres on utilise les termes père et fils pour désigner respectivement un antécédent et les descendants.
Ainsi, avec ces définitions :
Tous les noeuds qui ne sont pas des feuilles sont appelés des noeuds internes (et le feuilles parfois appelées des noeuds externes).
L'intérêt des arbres est d'y stocker de l'information. Pour cela, chaque noeud peut contenir une ou plusieurs valeurs. L'information portée par un noeud s'appelle l'étiquette du noeud (ou la valeur, ou la clé).
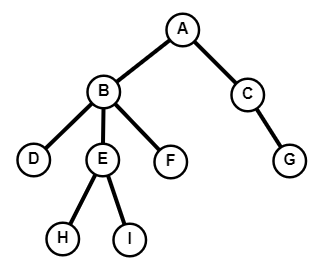
Dans cet arbre :
⚠️ Attention : On trouve aussi dans la littérature, que la profondeur de la racine est égale à 1, ce qui modifie la hauteur de l'arbre également puisqu'alors l'arbre réduit à la racine a pour hauteur 1 et l'arbre vide a pour hauteur 0. Les deux définitions se valent, il faut donc bien lire celle qui est donnée.

Dans la suite, on ne s'intéressera qu'aux arbres dont les noeuds ont au plus deux fils.
Seuls les arbres binaires sont au programme de Terminale NSI.
Un arbre binaire est un arbre dont tous les noeuds ont au plus deux fils.
L'arbre vu dans le paragraphe précédent n'est pas binaire car le noeud B possède 3 fils.
En revanche, l'arbre suivant est binaire.
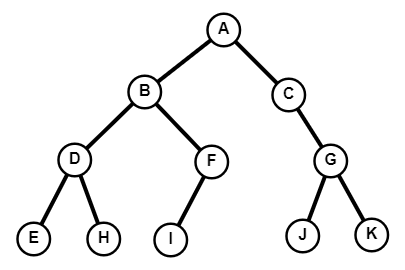
Les définitions vues précédemment pour des arbres quelconques restent bien évidemment valables pour les arbres binaires. Dans le cas d'un arbre binaire, chaque noeud possède deux sous-arbres, éventuellement vides, que l'on appelle sous-arbre gauche et sous-arbre droit.
Par exemple, dans le cas de l'arbre binaire précédent, le noeud A possède un sous-arbre gauche et un sous-arbre droit comme la figure suivante le montre.
![sous arbres gauche et droit]](data/ss_arbres.png)
Les sous-arbres gauche et droit de A sont eux-mêmes des arbres dont les racines sont respectivement B et C. Ces noeuds possèdent eux-même des sous-arbres gauche et droit. Par exemple, le noeud C possède un sous-arbre gauche, qui est vide, et un sous-arbre droit qui est l'arbre dont la racine est G. Ainsi de suite...
✏️ Faites tous les exercices proposés dans le notebook d'exercices.
Ce qui suit est un résumé de ce qui a été vu dans les exercices.
Arbre binaireDe manière générale, on peut construire un arbre binaire comme un noeud composé de deux sous-arbres. L'arbre vide est représentée par la valeur None. Ainsi, une feuille est un noeud avec les sous-arbres gauche et droit à None. Pour annoter la structure de l'arbre avec des informations, on utilise des étiquettes pouvant être enregistrées à chaque noeud.
On peut ensuite parcourir un arbre par l'accès à son étiquette et à ses sous-arbres droit et gauche. Un prédicat permet de distinguer les feuilles des noeuds.
On peut ainsi spécifier un arbre binaire par le type abstrait suivant :
noeud : Etiquette x Arbre binaire x Arbre binaire -> Arbre binairedroit : Arbre binaire -> Arbre binairegauche : Arbre binaire -> Arbre binaireetiquette : Arbre binaire -> Etiquetteest_feuille : Arbre binaire -> BooléenIl existe, comme toujours, plusieurs implémentations possibles d'un arbre binaire. Une implémentation classique consiste à représenter chaque noeud comme un objet d'une classe Noeud.
class Noeud:
def __init__(self, e, g=None, d=None):
self.etiquette = e
self.gauche = g
self.droit = d
def est_feuille(self):
return not self.gauche and not self.droit
# Une représentation possible de l'arbre
def __repr__(self):
ch = str(self.etiquette)
if self.gauche or self.droit:
ch = ch + '-(' + str(self.gauche) + ',' + str(self.droit) + ')'
return ch Il y a une petite subtilité à bien comprendre pour la méthode
__init__: on a choisi de définir la valeurNonepar défaut aux argumentsgaucheetdroit. Cela permet de construire une feuille (d'étiquette'a') en écrivantNoeud('a')au lieu de
Noeud('a', None, None).
La construction d'un arbre s'effectue alors avec des noeuds ayant soit un seul argument (cas des feuilles), soit trois (cas général).
>>> A1 = Noeud(2, Noeud(8, Noeud(4), Noeud(5)), Noeud(9, None, Noeud(3)))
>>> A1
2-(8-(4,5),9-(None,3))L'arbre A1 ainsi construit représente l'arbre binaire ci-dessous.
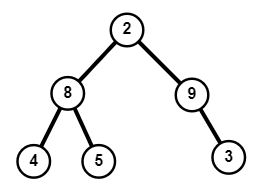
La définition d'un arbre binaire étant récursive, il est naturel d'écrire des algorithmes récursifs pour effectuer des opérations sur les arbres binaires.
En particulier, on peut écrire assez facilement deux fonctions récursives taille et hauteur qui calculent respectivement la taille et la hauteur d'un arbre binaire. Il suffit de parcourir récursivement l'arbre avec les méthodes gauche et droit.
def taille(A):
"""Renvoie la taille d'un arbre binaire A."""
if A is None:
return 0
else:
return 1 + taille(A.gauche) + taille(A.droit)
def hauteur(A):
"""Renvoie la hauteur d'un arbre binaire A"""
if A is None:
return -1
else:
return 1 + max(hauteur(A.gauche), hauteur(A.droit))On obtient alors :
>>> taille(A1)
6
>>> hauteur(A1)
2La hauteur d'un arbre binaire est la profondeur maximale de ses noeuds. Cependant un arbre binaire d'une taille donnée peut avoir un aspect totalement différent. En effet, les deux arbres binaires suivants sont de même taille (égale à 7) mais ont des "formes" très différentes.
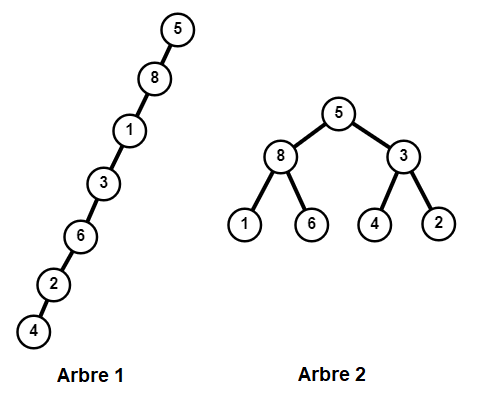
Le premier est dit filiforme ou dégénéré tandis que le second est dit parfait (un arbre est dit parfait si tous les niveaux sont remplis c'est-à-dire si chaque noeud interne a exactement deux fils).
Si on cherche à encadrer la hauteur d'un arbre binaire, ces deux exemples fournissent les deux cas de figure extrêmes :
De manière générale, on a l'encadrement suivant.
Si on note $H$ la hauteur d'un arbre binaire à $N$ noeuds, alors :
$$ \left \lfloor \log_2(N) \right \rfloor \leq H \leq N - 1,$$
où $\left \lfloor \log_2(N) \right \rfloor$ est la partie entière du logarithme en base 2 de $N$, c'est-à-dire le nombre de bits nécessaire à son écriture en base 2 diminué d'une unité (c'est la définition des informaticiens).
Cette propriété est expliquée dans un exercice.
On peut vérifier cela avec les arbres précédents de taille $N = 7$.
Ces deux arbres étant les cas extrêmes, un arbre binaire à 7 noeuds a une hauteur comprise entre 2 et 6.
Les applications des arbres sont nombreuses en informatique. Citons par exemple :
Références :
Germain BECKER, Lycée Mounier, ANGERS
Ressource éducative libre distribuée sous Licence Creative Commons Attribution - Pas d’Utilisation Commerciale - Partage dans les Mêmes Conditions 4.0 International

Voir en ligne : info-mounier.fr/terminale_nsi/structures_donnees/arbres